Bài 20: Một siêu thị thu được các số liệu sau đây về số tiền (đơn vị: nghìn đồng) mà mỗi người đã mua ở đây:
|
Lớp |
Giá trị đại diện |
Tần số |
|
[0, 99) |
|
20 |
|
[100, 199) |
|
80 |
|
[200, 299) |
|
70 |
|
[300, 399) |
|
30 |
|
[400, 499) |
|
10 |
|
|
|
N = 210 |
a) Dấu hiệu điều tra ở đây là gì?
b) Tìm số trung bình, phương sai và đọ lệch chuẩn (chính xác đến hàng phần trăm).
Đáp án
a) Dấu hiệu: Số tiền mua hàng
Đơn vị điều tra: Một hành khách mua hàng trong siêu thị
|
Lớp |
Giá trị đại diện |
Tần số |
|
[0, 99) |
49,5 |
20 |
|
[100, 199) |
149,5 |
80 |
|
[200, 299) |
249,5 |
70 |
|
[300, 399) |
349,5 |
30 |
|
[400, 499) |
449,5 |
10 |
|
|
|
N = 210 |
b) Ta có:
\(\overline x = 216,17\) nghìn đồng
\(s^2≈ 9841,27\)
\(s ≈ 99, 20\) nghìn đồng
Bài 21: Tuổi của 60 cán bộ trong một cơ quan được thống kê và trình bày trong bảng phân bố tần số ghép lớp sau:
|
Lớp |
Tần số |
|
[20, 30) |
13 |
|
[30, 40) |
26 |
|
[40, 50) |
15 |
|
[50, 60) |
6 |
|
|
N = 60 |
a) Dấu hiệu và đơn vị điều tra ở đây là gì?
b) Tìm số trung bình
Advertisements (Quảng cáo)
c) Lập bảng phân bố tần số – tần suất ghép lớp
d) Vẽ biểu đồ tần số hình cột
e) Tìm phương sai và độ lệch chuẩn (chính xác đến hàng phần trăm).
Đáp án
a) Dấu hiệu: Tuổi của một cán bộ
Đơn vị điều tra: Một cán bộ
b) Bảng phân bố tần số – tấn suất ghép lớp
Advertisements (Quảng cáo)
|
Lớp |
Giá trị đại diện |
Tần số |
Tần suất |
|
[20, 30) |
25 |
13 |
21,67 |
|
[30, 40) |
35 |
26 |
43,33 |
|
[40, 50) |
45 |
15 |
25 |
|
[50, 60) |
55 |
6 |
10 |
|
|
|
N = 60 |
|
c) Số trung bình: \(\overline x \approx 37,33\)
d) Phương sai: s2 ≈ 81,22
Độ lệch chuẩn là s ≈ 9,01
e) Biểu thị tần số hình cột
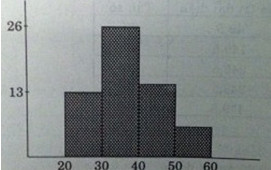
f) Trước hết, ta tính các góc ở tâm tương ứng với tần suất của các lớp (xem bảng sau).
Từ đó, vẽ được biểu đồ tần suất hình quạt
|
Lớp |
Góc ở tâm |
|
[20, 30) |
780 |
|
[30, 40) |
1560 |
|
[40, 50) |
900 |
|
[50, 60) |
360 |
Bài 22: a) Biết \(\sin \alpha = {2 \over 3};\,\,\cos \beta = – {3 \over 4}\) và các điểm trên đường tròn lượng giác xác định bởi α và β nằm ở góc phần tư thứ II. Hãy tính sin (α + β); cos(α + β); sin(α – β); cos(α – β)
b) Cho \(\sin 2\alpha = – {4 \over 5}\,\,;\,\,\,{\pi \over 2} < \alpha < {{3\pi } \over 4}\) . Hãy tính các giá trị lượng giác của góc α
Đáp án
a) Vì α và β nằm ở góc phần tư thứ II nên sinβ > 0; cos α < 0
Do đó:
\(\eqalign{
& \cos \alpha = – \sqrt {1 – {{\sin }^2}\alpha } = – \sqrt {1 – {4 \over 9}} = – {{\sqrt 5 } \over 3} \cr
& \sin \beta = \sqrt {1 – {{\cos }^2}\beta } = \sqrt {1 – {9 \over {16}}} = {{\sqrt 7 } \over 4} \cr} \)
Từ đó:
\(\eqalign{
& \cos (\alpha + \beta ) = \cos \alpha \cos \beta – \sin \alpha \sin \beta \cr&= {{3\sqrt 5 – 2\sqrt 7 } \over {12}} \cr
& \sin (\alpha + \beta ) = \sin \alpha \cos \beta + \cos \alpha \sin \beta \cr&= – {{6 + \sqrt {35} } \over {12}} \cr
& \cos (\alpha – \beta ) = \cos \alpha \cos \beta + \sin \alpha \sin \beta \cr&= {{3\sqrt 5 + 2\sqrt 7 } \over {12}} \cr
& \sin (\alpha – \beta ) = \sin \alpha \cos \beta – \cos \alpha \sin \beta \cr&= {{ – 6 + \sqrt {35} } \over {12}} \cr} \)
b) Do \({\pi \over 2} < \alpha < {{3\pi } \over 4} \Rightarrow \pi < 2\alpha < {{3\pi } \over 2}\)
Suy ra: cos2α < 0; sinα > 0 và cosα < 0
Vậy:
\(\eqalign{
& \cos 2\alpha = – \sqrt {1 – {{\sin }^2}2\alpha } = – {3 \over 5} \cr
& 2{\sin ^2}\alpha = 1 – \cos 2\alpha = 1 + {3 \over 5} = {8 \over 5} \Rightarrow \sin \alpha = {2 \over {\sqrt 5 }} \cr
& \cos \alpha = – \sqrt {{{1 + \cos 2\alpha } \over 2}} = – \sqrt {{1 \over 5}} = – {1 \over 5} \cr
& \tan \alpha = – 2 \cr
& \cot \alpha = – {1 \over 2} \cr} \)

