Bài 2 Chuyển động thẳng đều Sách bài tập Vật lí 10. Giải bài 2.15, 2.16, 2.17 trang 10 Sách bài tập Vật lí 10. Câu 2.15: Một người đứng tại điểm M cách con đường thẳng AB một đoạn h = 50 m để chờ ô tô…
Bài 2.15: Một người đứng tại điểm M cách con đường thẳng AB một đoạn h = 50 m để chờ ô tô.Khi nhìn thấy ô tô còn cách mình một đoạn L = 200 m thì người đó bắt đầu chay ra đường để bắt kịp ô tô (Hình 2.3). Vận tốc của ô tô là v1 = 36 km/h. Nếu người đó chạy với vận tốc v2 = 12 km/h thì phải chạy theo hướng nào để gặp đúng lúc ô tô vừa tới ?
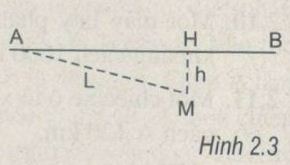
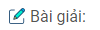
Giả sử người đó gặp ô tô tại điểm N. Khoảng thời gian t để người đó chạy từ M tới N phải đúng bằng khoảng thời gian để ô tô chạy từ A tới N
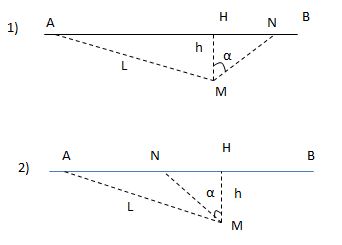Ta có: AN = v1t = 36t
MN – v2t = 12t
\(AH = \sqrt {{L^2} – {h^2}} = 0,19365(km)\)
\(HN = \sqrt {M{N^2} – {h^2}} = \sqrt {{{12}^2}{t^2} – 0,{{05}^2}}\)
Cả hai trường hợp, đều có HN2 = MN2 – h2
Cuối cùng ta được phương trình bậc hai 1152t2 – 13,9428t + 0,04 = 0
Advertisements (Quảng cáo)
Giải ra ta được hai nghiệm: t = 0,00743 h ≈ 26,7 s hoặc t = 0,00467 h ≈ 16,8 s
Do đó AN = 0,26748 km hoặc AN = 0,16812 km
Quãng đường MN mà người ấy phải chạy là MN = 89,2 m hoặc MN = 56 m
Gọi α là góc hợp bởi MN và MH:
\(cos {\alpha _1} = {h \over {MN}} = {{50} \over {89,2}} \approx 0,5605 = > {\alpha _1} \approx {55^0}54’\)
\(cos {\alpha _2} = {h \over {MN}} = {{50} \over {56}} \approx 0,5605 = > {\alpha _1} \approx {26^0}46’\)
Advertisements (Quảng cáo)
Bài 2.16: Một ô tô chạy trên một đoạn đường thẳng từ địa điểm A đến địa điểm B phải mất một khoảng thời gian t. Tốc độ của ồ tô trong nửa đầu của khoảng thời gian này là 60 km/h và trong nửa cuối là 40 km/h. Tính tốc độ trung bình của ô tô trên cả đoạn đường AB.
+ Do nửa đầu của khoảng thời gian đó xe chạy với tốc độ v1 = 60 km/s => quãng đường đi được là s1 = v1.t/2 = 30t
+ Do nửa cuối của khoảng thời gian đó xe chạy với tốc độ v2 = 40 km/h => quãng đường đi được là s2 = v2.t/2 = 20t
=> Độ dài quãng đường AB là s = s1 + s2 = 50t
=> Tốc độ trung bình trên cả quãng đường AB là vtb = s/t = 50 km/h
Bài 2.17: Một người đi xe đạp chuyển động trên một đoạn đường thẳng AB có độ dài là s. Tốc độ của xe đạp trong nửa đầu của đoạn đường này là 12 km/h và trong nửa cuối là 18 km/h. Tính tốc độ trung bình của xe đạp trên cả đoạn đường AB.
Gọi thời gian đi hết nửa đầu và nửa cuối đoạn đường AB là t1 và t2
+ Do nửa đầu đoạn đường xe đạp đi với vận tốc v1 nên \({t_1} = {{{s_1}} \over {{v_1}}} = {s \over {2{v_1}}}\)
+ Do nửa cuối quãng đường xe đạp đi với vận tốc v2 nên \({t_2} = {{{s_2}} \over {{v_2}}} = {s \over {2{v_2}}}\)
=> Thời gian đi hết đoạn đường AB là
\(t = {t_1} + {t_2} = {s \over {2{v_1}}} + {s \over {2{v_2}}}\)
=> Tốc độ trung bình trên cả đoạn đường AB là
\({v_{tb}} = {s \over t} = {s \over {{s \over {2{v_1}}} + {s \over {2{v_2}}}}} = {1 \over {{1 \over {2{v_1}}} + {1 \over {2{v_2}}}}} = {1 \over {{1 \over {2.12}} + {1 \over {2.18}}}} = 14,4(km/h)\)
