Bài Đề toán tổng hợp chương III phần hình học Sách bài tập Toán Hình học 10. Giải bài 5, 6, 7, 8 trang 197 Sách bài tập Toán Hình học 10. Câu 5: Trong mặt phẳng Oxy cho đường tròn (T) có phương trình…
Bài 5: Trong mặt phẳng Oxy cho đường tròn (T) có phương trình:
\({x^2} + {y^2} – 4x – 2y + 3 = 0\)
a) Tìm tọa độ tâm và tính bán kính của đường tròn (T).
b) Tìm m để đường thẳng y = x + m có điểm chung với đường tròn (T).
c) Viết phương trình tiếp tuyến \(\Delta \) với đường tròn (T) biết rằng \(\Delta \) vuông góc vơi đường thẳng d có phương trình \x – y + 2006 = 0.

a) Đường tròn (T) có tâm là điểm (2 ; 1) và có bán kính bằng \(\sqrt 2 \)
b) Đường thẳng \(l:x – y + m = 0\). Ta có :
\(l\) có điểm chung với (T)
\( \Leftrightarrow d(I,l) \le R\)
\( \Leftrightarrow {{\left| {2 – 1 + m} \right|} \over {\sqrt 2 }} \le \sqrt 2 \)
\(\eqalign{
& \left| {m + 1} \right| \le 2 \Leftrightarrow – 2 \le m + 1 \le 2 \cr
& \Leftrightarrow – 3 \le m \le 1. \cr} \)
c) \(\Delta \bot d\) nên \(\Delta \) có phương trình x + y + c = 0.
Ta có : \(\Delta \) tiếp xúc với (T) khi và chỉ khi:
\(d(I,\Delta ) = R\)
\(\eqalign{
& \Leftrightarrow {{\left| {2 + 1 + c} \right|} \over {\sqrt 2 }} = \sqrt 2 \Leftrightarrow \left| {c + 3} \right| = 2 \cr
& \Leftrightarrow \left[ \matrix{
c + 3 = 2 \hfill \cr
c + 3 = – 2 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
c = – 1 \hfill \cr
c = – 5 \hfill \cr} \right. \cr} \)
Vậy có hai tiếp tuyến với (T) thỏa mãn đề bài là :
\({\Delta _1}:x + y – 1 = 0\)
\({\Delta _2}:x + y – 5 = 0.\)
Bài 6: Trong mặt phẳng Oxy cho elip (E) có tiêu điểm thứ nhất là \(\left( { – \sqrt 3 ;0} \right)\) và đi qua điểm \(M\left( {1;{{\sqrt 3 } \over 2}} \right)\)
a) Hãy xác định tọa độ các đỉnh của (E).
b) Viết phương trình chính tắc của (E).
c) Đường thẳng đi qua tiêu điểm thứ hai của elip (E) và vuông góc với trục Ox và cắt (E) tại hai điểm C và D. Tính độ dài đoạn thẳng CD.

a) (E) có tiêu điểm \({F_1}\left( { – \sqrt 3 ;0} \right)\) nên \(c = \sqrt 3 .\)
Phương trình chính tăc của (E) có dạng
Advertisements (Quảng cáo)
\({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1.\)
Ta có : \(M\left( {1;{{\sqrt 3 } \over 2}} \right) \in (E)\)
\( \Rightarrow {1 \over {{a^2}}} + {3 \over {4{b^2}}} = 1\,\,\,\,\,\,\,\,\,\,(1)\)
Và \({a^2} = {b^2} + {c^2} = {b^2} + 3\)
Thay vào (1) ta được :
\(\eqalign{
& {1 \over {{b^2} + 3}} + {3 \over {4{b^2}}} = 1 \cr
& \Leftrightarrow 4{b^2} + 3{b^2} + 9 = 4{b^2}(b + 3) \cr} \)
\( \Leftrightarrow 4{b^4} + 5{b^2} – 9 = 0 \Leftrightarrow {b^2} = 1\)
Suy ra \({a^2} = 4.\)
Ta có a = 2 ; b = 1.
Vậy (E) có bốn đỉnh là : (-2 ; 0), (2 ; 0)
(0 ; -1) và (0 ; 1).
b) Phương trình chính tắc của (E) là :
\({{{x^2}} \over 4} + {{{y^2}} \over 1} = 1\)
c) (E) có tiêu điểm thứ hai là điểm \(\left( {\sqrt 3 ;0} \right)\). Đường thẳng \(\Delta \) đi qua điểm \(\left( {\sqrt 3 ;0} \right)\) và vuông góc với Ox có phương trình \(x = \sqrt 3 .\)
Phương trình tung độ giao điểm của \(\Delta \) và (E) là :
\({3 \over 4} + {{{y^2}} \over 1} = 1 \Leftrightarrow {y^2} = \pm {1 \over 2}.\)
Suy ra tọa độ của C và D là :
Advertisements (Quảng cáo)
\(C\left( {\sqrt 3 ; – {1 \over 2}} \right)\) và \(\left( {\sqrt 3 ;{1 \over 2}} \right)\)
Vậy CD = 1.
Bài 7: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({x^2} + {y^2} – 6x – 6y + 14 = 0\). Tìm điểm M thuộc trục hoành sao cho từ M kẻ được hai tiếp tuyến của (C) mà góc giữa hai tiếp tuyến đó bằng \({60^ \circ }\).

(Xem hình 3.30)
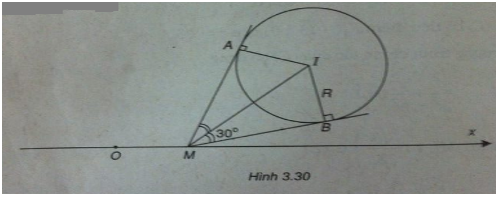
Đường tròn (C) có tâm I(3 ; 3) và có bán kính
\(R = \sqrt {{a^2} + {b^2} – c} = \sqrt {9 + 9 – 14} = 2\)
Điểm M(x;0) thuộc Ox.
Từ M kẻ hai tiếp tuyến tiếp xúc với (C) tại A và B. Ta có:
\(\widehat {AMB} = {60^ \circ } \Rightarrow \widehat {IMB} = {30^ \circ }\)
\( \Rightarrow IM = {R \over {\sin {{30}^ \circ }}} = 2R = 4\)
\(IM = 4 \Leftrightarrow \sqrt {{{\left( {x – 3} \right)}^2} + 9} = 4\)
\( \Leftrightarrow {x^2} – 6x + 2 = 0\)
\( \Leftrightarrow x = 3 \pm \sqrt 7 \)
Vậy có hai điểm M thỏa mãn đề bài, chúng có tọa độ là :
\({M_1}\left( {3 + \sqrt 7 ;0} \right)\) và \({M_2}\left( {3 – \sqrt 7 ;0} \right)\)
Bài 8: Cho đường tròn (C) tâm I(1 ; -2), bán kính R và điểm K(1 ; 3).
a) Cho R = 1. Viết phương trình tiếp tuyến của (C) đi qua K;
b) Xác định R để từ K vẽ được đến (C) hai tiếp tuyến tiếp xúc với (C) lần lượt tại hai điểm \({M_1},{M_2}\) sao cho diện tích tứ giác \(K{M_1}I{M_2}\) bằng \(2\sqrt 6 \).

(Xem hình 3.31)

a) R = 1. Gọi \(\Delta \) là đường thẳng đi qua điểm K(1 ; 3) và có hệ số góc m. \(\Delta \) có phương trình y = m(x – 1) + 3
\( \Leftrightarrow mx – y + (3 – m) = 0.\)
Ta có \(\Delta \) tiếp xúc vơi (C) \( \Leftrightarrow d(I,\Delta ) = R\)
\( \Leftrightarrow {{\left| {m + 2 + 3 – m} \right|} \over {\sqrt {{m^2} + 1} }} = 1 \Leftrightarrow {5 \over {\sqrt {{m^2} + 1} }} = 1\)
\( \Leftrightarrow {m^2} + 1 = 25\)
\( \Leftrightarrow m = \pm 2\sqrt 6 \)
Vậy qua điểm K có hai tiếp tuyến với (C). Đó là :
\({\Delta _1}:y = 2\sqrt 6 \left( {x – 1} \right) + 3\) và \({\Delta _2}:y = – 2\sqrt 6 \left( {x – 1} \right) + 3.\)
b) Ta có: \(KI = \sqrt {{{\left( {1 – 1} \right)}^2} + {{\left( {3 + 2} \right)}^2}} = 5\)
\(K{M_2} = \sqrt {K{I^2} – {R^2}} = \sqrt {25 – {R^2}} .\)
Ta có : \({S_{K{M_1}I{M_2}}} = 2\sqrt 6 \)
\( \Leftrightarrow 2{S_{I{M_2}K}} = 2\sqrt 6 \)
\( \Leftrightarrow I{M_2}.K{M_2} = 2\sqrt 6 \)
\( \Leftrightarrow R\sqrt {25 – {R^2}} = 2\sqrt 6 \)
\( \Leftrightarrow {R^2}\left( {25 – {R^2}} \right) = 24\)
\(\Leftrightarrow {R^4} – 25{R^2} + 24 = 0\)
\( \Leftrightarrow \left[ \matrix{
{R^2} = 1 \hfill \cr
{R^2} = 24 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
R = 1 \hfill \cr
R = 2\sqrt 6 \hfill \cr} \right.\)
Vậy bán kính đường tròn bằng 1 hoặc \(2\sqrt 6 .\)

