Bài 4: Một hình lục giác đều ABCDEF (các đỉnh lấy theo thứ tự đó và ngược chiều quay của kim đồng hồ) nội tiếp trong đường tròn tâm O. Tính số bằng rađian của các cung lượng giác: cung AB, AC, AD, AE, AF.

(h.63)
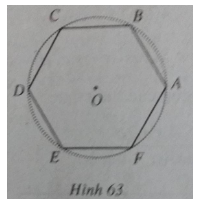
Sđ cung \(AB = {\pi \over 3} + k2\pi ,k \in Z\)
Sđ cung \(AC = {{2\pi } \over 3} + k2\pi ,k \in Z\)
Sđ cung \(A{\rm{D}} = \pi + k2\pi ,k \in Z\)
Sđ cung \(A{\rm{E}} = {{4\pi } \over 3} + k2\pi ,k \in Z\)
Advertisements (Quảng cáo)
Sđ cung \(AF = {{5\pi } \over 3} + k2\pi ,k \in Z\)
Bài 5: Cho cung lượng giác AB có số đo là 15 rad. Tìm số lớn nhất trong các số đo của cung lượng giác điểm đầu A, điểm cuối B, có số đo âm.

Ta có Sđ cung \(AB = 15 + k2\pi ,k \in Z\)
Advertisements (Quảng cáo)
\(15 + k2\pi < 0 \Leftrightarrow k < – {{15} \over {2\pi }}\)
Vậy với k = -3 ta được cung AB có số đo âm lớn nhất là \(15 – 6\pi \)
Bài 6: Tìm số x \((0 \le x \le 2\pi )\) và số nguyên k sao cho \(a = x + k2\pi \) trong các trường hợp
a) \(a = 12,4\pi \);
b) \(a = – {9 \over 5}\pi \);
c) \(a = {{13} \over 4}\pi \).

Đáp số:
a) \(x = 0,4\pi ;k = 6\);
b) \(x = {\pi \over 5};k = – 1\);
c) \(x = {{5\pi } \over 4};k = 1\).

