Bài 3.26: Hình chóp S.ABCD có đáy là hình thoi ABCD cạnh a và có SA = SB = SC = a. Chứng minh:
a) Mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD)
b) Tam giác SBD là tam giác vuông tại S.
a) Gọi O là tâm của hình thoi, ta có \(AC \bot BD\) tại O
Vì SA = SC nên \(SO \bot AC\).
Do đó AC vuông góc với mặt phẳng (SBD)
Ta suy ra mặt phẳng (ABCD) vuông góc với mặt phẳng (SBD).
b) Ba tam giác SAC, BAC, DAC bằng nhau ( c.c.c) nên ta suy ra OS = OB = OD. Vậy tam giác SBD vuông tại S.
Bài 3.27: a) Cho hình lập phương ABCD.A’B’C’D’ cạnh a. Chứng minh rằng đường thẳng AC’ vuông góc với mặt phẳng (A’BD) và mặt phẳng (ACC’A’) vuông góc với mặt phẳng (A’BD).
b) Tính đường chéo AC’ của hình lập phương đã cho.
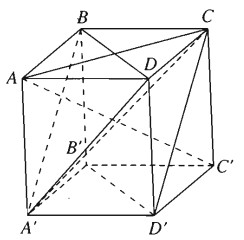
a) Ta có \(AB = A{\rm{D}} = AA’ = a\)
Advertisements (Quảng cáo)
và \(C’B = C’D = C’A’ = a\sqrt 2 \)
Vì hai điểm A và C’ cách đều ba đỉnh của tam giác A’BD nên A và C’ thuộc trục đường tròn ngoại tiếp tam giác BDA’ . Vậy \(AC’ \bot \left( {B{\rm{D}}A’} \right)\). Mặt khác vì mặt phẳng (ACC’A’) chứa đường thẳng AC’ mà \(AC’ \bot \left( {B{\rm{D}}A’} \right)\) nên ta suy ra mặt phẳng (ACC’A’) vuông góc với mặt phẳng (BDA’)
b) Ta có ACC’ là tam giác vuông có cạnh \(AC = a\sqrt 2 \) và CC’ = a
Vậy \(AC{‘^2} = A{C^2} + CC{‘^2} \Rightarrow AC{‘^2} = 2{{\rm{a}}^2} + {a^2} = 3{{\rm{a}}^2}\)
Vậy \(AC’ = a\sqrt 3 \).
Bài 3.28: Cho hình chóp đều S.ABC. Chứng minh
a) Mỗi cạnh bên của hình chóp đó vuông góc với cạnh đối diện ;
b) Mỗi mặt phẳng chứa một cạnh bên và đường cao của hình chóp đều vuông góc với cạnh đối diện.
Advertisements (Quảng cáo)
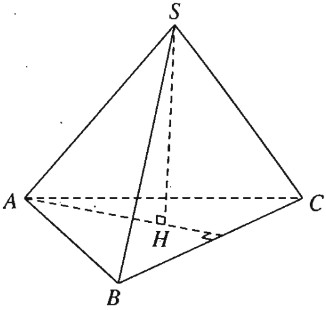
a) Vì S.ABC là hình chóp đều nên ∆ABC là tam giác đều và có SA = SB = SC. Do đó khi ta vẽ \(SH \bot \left( {ABC} \right)\) thì H là trọng tâm của tam giác đều ABC và ta có \(AH \bot BC\). Theo định lí ba đường vuông góc ta có \(SA \bot BC\).
Chứng minh tương tự ta có \(SB \bot AC\) và \(SC \bot AB\)
b) Vì \(BC \bot AH\) và \(BC \bot SH\) nên \(BC \bot \left( {SAH} \right)\)
Chứng minh tương tự ta có \(CA \bot \left( {SBH} \right)\) và \(AB \bot \left( {SCH} \right)\).
Bài 3.29: Tứ diện SABC có SA vuông góc với mặt phẳng (ABC). Gọi H và K lần lượt là trực tâm của các tam giác ABC và SBC. Chứng minh rằng:
a) AH, SK và BC đồng quy.
b) SC vuông góc với mặt phẳng (BHK) và \(\left( {SAC} \right) \bot \left( {BHK} \right)\)
c) HK vuông góc với mặt phẳng (SBC) và \(\left( {SBC} \right) \bot \left( {BHK} \right)\)
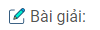
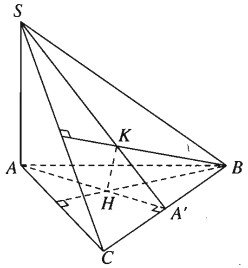
a) Gọi A’ là giao điểm của AH và BC. Ta cần chứng minh ba điểm S, K, A’ thẳng hàng.
Vì H là trực tâm của tam giác ABC nên \(AA’ \bot BC\). Mặt khác theo giả thiết ta có: \(SA \bot \left( {ABC} \right)\), do đó \(SA \bot BC\). Từ đó ta suy ra \(BC \bot \left( {SAA’} \right)\) và \(BC \bot SA’\). Vậy SA’ là đường cao của tam giác SBC nên SA’ là phải đi qua trực tâm K. Vậy ba đường thẳng AH, SK và BC đồng quy.
b) Vì K là trực tâm của tam giác SBC nên \(BK \bot SC\,\,\,\,\,\,\,\,\left( 1 \right)\)
Mặt khác ta có \(BH \bot AC\) vì H là trực tâm của tam giác ABC và \(BH \bot SA\) vì \(SA \bot \left( {ABC} \right)\).
Do đó \(BH \bot \left( {ABC} \right)\) nên \(BH \bot SC\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\).
Từ (1) và (2) ta suy ra \(SC \bot \left( {BHK} \right)\). Vì mặt phẳng (SAC) chứa SC mà \(SC \bot \left( {BHK} \right)\) nên ta có \(\left( {SAC} \right) \bot \left( {BHK} \right)\).
c) Ta có: \(\left. \matrix{
BC \bot \left( {SAA’} \right),BC \bot HK \hfill \cr
SC \bot \left( {BHK} \right),SC \bot HK \hfill \cr} \right\} \Rightarrow HK \bot \left( {SBC} \right)\)
Mặt phẳng (BHK) chứa HK mà \(HK \bot \left( {SBC} \right)\) nên \(\left( {BHK} \right) \bot \left( {SBC} \right)\).

