Câu 13: Quy đồng mẫu thức các phân thức:
a. \({{25} \over {14{x^2}y}},{{14} \over {21x{y^5}}}\)
b. \({{11} \over {102{x^4}y}},{3 \over {34x{y^3}}}\)
c. \({{3x + 1} \over {12x{y^4}}},{{y – 2} \over {9{x^2}{y^3}}}\)
d. \({1 \over {6{x^3}{y^2}}},{{x + 1} \over {9{x^2}{y^4}}},{{x – 1} \over {4x{y^3}}}\)
e. \({{3 + 2x} \over {10{x^4}y}},{5 \over {8{x^2}{y^2}}},{2 \over {3x{y^5}}}\)
f. \({{4x – 4} \over {2x\left( {x + 3} \right)}},{{x – 3} \over {3x\left( {x + 1} \right)}}\)
g. \({{2x} \over {{{\left( {x + 2} \right)}^3}}},{{x – 2} \over {2x{{\left( {x + 2} \right)}^2}}}\)
h. \({5 \over {3{x^3} – 12x}},{3 \over {\left( {2x + 4} \right)\left( {x + 3} \right)}}\)

a. MTC \( = 42{x^2}{y^5}\)
\({{14} \over {21x{y^5}}} = {2 \over {3x{y^5}}}\)\( = {{2.14x} \over {3x{y^5}.14x}} = {{28x} \over {42{x^2}{y^5}}}\); \({{25} \over {14{x^2}y}} = {{25.{3y^4}} \over {14{x^2}y.{3y^4}}} = {{75{y^4}} \over {42{x^2}{y^5}}}\)
b. MTC = \(102{x^4}{y^3}\)
\({{11} \over {102{x^4}y}} = {{11.{y^2}} \over {102{x^4}y.{y^2}}} = {{11{y^2}} \over {102{x^4}{y^3}}}\); \({3 \over {34x{y^3}}} = {{3.3{x^3}} \over {34x{y^3}.3{x^3}}} = {{9{x^3}} \over {102{x^4}{y^3}}}\)
c. MTC = \(36{x^2}{y^4}\)
\({{3x + 1} \over {12x{y^4}}} = {{\left( {3x + 1} \right).3x} \over {12x{y^4}.3x}} = {{9{x^2} + 3x} \over {36{x^2}{y^4}}}\); \({{y – 2} \over {9{x^2}{y^3}}} = {{\left( {y – 2} \right).4y} \over {9{x^2}{y^3}.4y}} = {{4{y^2} – 8y} \over {36{x^2}{y^4}}}\)
d. MTC = \(36{x^3}{y^4}\)
\({1 \over {6{x^3}{y^2}}} = {{1.6{y^2}} \over {6{x^3}{y^2}.6{y^2}}} = {{6{y^2}} \over {36{x^3}{y^4}}}\); \({{x + 1} \over {9{x^2}{y^4}}} = {{\left( {x + 1} \right).4x} \over {9{x^2}{y^4}.4x}} = {{4{x^2} + 4x} \over {36{x^3}{y^4}}}\)
\({{x – 1} \over {4x{y^3}}} = {{\left( {x – 1} \right).9{x^2}y} \over {4x{y^3}.9{x^2}y}} = {{9{x^3}y – 9{x^2}y} \over {36{x^3}{y^4}}}\)
e. MTC = \(120{x^4}{y^5}\)
\({{3 + 2x} \over {10{x^4}y}} = {{\left( {3 + 2x} \right).12{y^4}} \over {10{x^4}y.12{y^4}}} = {{36{y^4} + 24x{y^4}} \over {120{x^4}{y^5}}}\)
\({5 \over {8{x^2}{y^2}}} = {{5.15{x^2}{y^3}} \over {8{x^2}{y^2}.15{x^2}{y^3}}} = {{75{x^2}{y^3}} \over {120{x^4}{y^5}}}\)
Advertisements (Quảng cáo)
\({2 \over {3x{y^5}}} = {{2.40{x^3}} \over {3x{y^5}.40{x^3}}} = {{80{x^3}} \over {120{x^4}{y^5}}}\)
f. MTC = \(3x\left( {x + 3} \right)\left( {x + 1} \right)\) Vì \({{4x – 4} \over {2x\left( {x + 3} \right)}} = {{2\left( {x – 1} \right)} \over {x\left( {x + 3} \right)}}\)
\({{4x – 4} \over {2x\left( {x + 3} \right)}} = {{2\left( {x – 1} \right)} \over {x\left( {x + 3} \right)}} = {{2\left( {x – 1} \right).3\left( {x + 1} \right)} \over {x\left( {x + 3} \right).3\left( {x + 1} \right)}} = {{6\left( {{x^2} – 1} \right)} \over {3x\left( {x + 3} \right)\left( {x + 1} \right)}}\)
\({{x – 3} \over {3x\left( {x + 1} \right)}} = {{\left( {x – 3} \right)\left( {x + 3} \right)} \over {3x\left( {x + 1} \right)\left( {x + 3} \right)}} = {{{x^2} – 9} \over {3x\left( {x + 1} \right)\left( {x + 3} \right)}}\)
g. MTC = \(2x{\left( {x + 2} \right)^3}\)
\({{2x} \over {{{\left( {x + 2} \right)}^3}}} = {{2x.2x} \over {2x{{\left( {x + 2} \right)}^3}}} = {{4{x^2}} \over {2x{{\left( {x + 2} \right)}^3}}}\)
\({{x – 2} \over {2x{{\left( {x + 2} \right)}^2}}} = {{\left( {x – 2} \right)\left( {x + 2} \right)} \over {2x{{\left( {x + 2} \right)}^2}\left( {x + 2} \right)}} = {{{x^2} – 4} \over {2x{{\left( {x + 2} \right)}^3}}}\)
h. \(3{x^3} – 12x = 3x\left( {{x^2} – 4} \right) = 3x\left( {x – 2} \right)\left( {x + 2} \right)\)
\(\left( {2x + 4} \right)\left( {x + 3} \right) = 2\left( {x + 2} \right)\left( {x + 3} \right)\)
MTC = \(6x\left( {x – 2} \right)\left( {x + 2} \right)\left( {x + 3} \right)\)
\(\eqalign{ & {5 \over {3{x^3} – 12x}} = {5 \over {3x\left( {x – 2} \right)\left( {x + 2} \right)}} = {{5.2\left( {x + 3} \right)} \over {3x\left( {x – 2} \right)\left( {x + 2} \right).2\left( {x + 3} \right)}} \cr & = {{10\left( {x + 3} \right)} \over {6x\left( {x – 2} \right)\left( {x + 2} \right)\left( {x + 3} \right)}} \cr & {3 \over {\left( {2x + 4} \right)\left( {x + 3} \right)}} = {3 \over {2\left( {x + 2} \right)\left( {x + 3} \right)}} = {{3.3x\left( {x – 2} \right)} \over {2\left( {x + 2} \right)\left( {x + 3} \right).3x\left( {x – 2} \right)}} \cr & = {{9x\left( {x – 2} \right)} \over {6x\left( {x + 2} \right)\left( {x – 2} \right)\left( {x + 3} \right)}} \cr} \)
Câu 14: Quy đồng mẫu thức các phân thức:
a. \({{7x – 1} \over {2{x^2} + 6x}},{{5 – 3x} \over {{x^2} – 9}}\)
b. \({{x + 1} \over {x – {x^2}}},{{x + 2} \over {2 – 4x + 2{x^2}}}\)
Advertisements (Quảng cáo)
c. \({{4{x^2} – 3x + 5} \over {{x^3} – 1}},{{2x} \over {{x^2} + x + 1}},{6 \over {x – 1}}\)
d. \({7 \over {5x}},{4 \over {x – 2y}},{{x – y} \over {8{y^2} – 2{x^2}}}\)
e. \({{5{x^2}} \over {{x^3} + 6{x^2} + 12x + 8}},{{4x} \over {{x^2} + 4x + 4}},{3 \over {2x + 4}}\)

a. \(2{x^2} + 6x = 2x\left( {x + 3} \right);{x^2} – 9 = \left( {x + 3} \right)\left( {x – 3} \right)\) MTC = \(2x\left( {x + 3} \right)\left( {x – 3} \right)\)
\(\eqalign{ & {{7x – 1} \over {2{x^2} + 6x}} = {{7x – 1} \over {2x\left( {x + 3} \right)}} = {{\left( {7x – 1} \right)\left( {x – 3} \right)} \over {2x\left( {x + 3} \right)\left( {x – 3} \right)}} \cr & {{5 – 3x} \over {{x^2} – 9}} = {{5 – 3x} \over {\left( {x + 3} \right)\left( {x – 3} \right)}} = {{2x\left( {5 – 3x} \right)} \over {2x\left( {x + 3} \right)\left( {x – 3} \right)}} \cr} \)
b. \(x – {x^2} = x\left( {1 – x} \right)\); \(2 – 4x + 2{x^2} = 2\left( {1 – 2x + {x^2}} \right) = 2{\left( {1 – x} \right)^2}\)
MTC = \(2x{\left( {1 – x} \right)^2}\)
\(\eqalign{ & {{x + 1} \over {x – {x^2}}} = {{x + 1} \over {x\left( {1 – x} \right)}} = {{\left( {x + 1} \right).2\left( {1 – x} \right)} \over {x\left( {1 – x} \right).2\left( {1 – x} \right)}} = {{2{{\left( {1 – x} \right)}^2}} \over {2x{{\left( {1 – x} \right)}^2}}} \cr & {{x + 2} \over {2 – 4x + 2{x^2}}} = {{x + 2} \over {2{{\left( {1 – x} \right)}^2}}} = {{\left( {x + 2} \right).x} \over {2x{{\left( {1 – x} \right)}^2}}} \cr} \)
c. \({x^3} – 1 = \left( {x – 1} \right)\left( {{x^2} + x + 1} \right)\) MTC = \({x^3} – 1\) \({{4{x^2} – 3x + 5} \over {{x^3} – 1}}\);
\(\eqalign{ & {{2x} \over {{x^2} + x + 1}} = {{2x\left( {x + 1} \right)} \over {\left( {{x^2} + x + 1} \right)\left( {x – 1} \right)}} = {{2x\left( {x – 1} \right)} \over {{x^3} – 1}} \cr & {6 \over {x – 1}} = {{6\left( {{x^2} + x + 1} \right)} \over {\left( {x – 1} \right)\left( {{x^2} + x + 1} \right)}} = {{6\left( {{x^2} + x + 1} \right)} \over {{x^3} – 1}} \cr} \)
d. \(8{y^2} – 2{x^2} = 2\left( {4{y^2} – {x^2}} \right) = 2\left( {2y + x} \right)\left( {2y – x} \right)\)
MTC = \(10x\left( {2y + x} \right)\left( {2y – x} \right)\)
\(\eqalign{ & {7 \over {5x}} = {{7.2\left( {2y + x} \right)\left( {2y – x} \right)} \over {5x.2\left( {2y + x} \right)\left( {2y – x} \right)}} = {{14\left( {2y + x} \right)\left( {2y – x} \right)} \over {10x\left( {2y + x} \right)\left( {2y – x} \right)}} \cr & {4 \over {x – 2y}} = {{ – 4} \over {2y – x}} = {{ – 4.10x\left( {2y + x} \right)} \over {\left( {2y – x} \right).10x\left( {2y + x} \right)}} = {{ – 40x\left( {2y + x} \right)} \over {10x\left( {2y + x} \right)\left( {2y – x} \right)}} \cr & {{x – y} \over {8{y^2} – 2{x^2}}} = {{x – y} \over {2\left( {2y + x} \right)\left( {2y – x} \right)}} = {{\left( {x – y} \right).5x} \over {2\left( {2y + x} \right)\left( {2y – x} \right).5x}} \cr & = {{5x\left( {x – y} \right)} \over {10x\left( {2y + x} \right)\left( {2y – x} \right)}} \cr} \)
e. \(\eqalign{ & {x^3} + 6{x^2} + 12x + 8 = {x^3} + 3{x^2}.2 + 3.x{.2^2} + {2^3} = {\left( {x + 2} \right)^3} \cr & {x^2} + 4x + 4 = {\left( {x + 2} \right)^2};2x + 4 = 2\left( {x + 2} \right) \cr} \)
MTC =\(2{\left( {x + 2} \right)^3}\)
\(\eqalign{ & {{5{x^2}} \over {{x^3} + 6{x^2} + 12x + 8}} = {{5{x^2}} \over {{{\left( {x + 2} \right)}^3}}} = {{5{x^2}.2} \over {{{\left( {x + 2} \right)}^3}.2}} = {{10{x^2}} \over {2{{\left( {x + 2} \right)}^3}}} \cr & {{4x} \over {{x^2} + 4x + 4}} = {{4x} \over {{{\left( {x + 2} \right)}^2}}} = {{4x.2\left( {x + 2} \right)} \over {{{\left( {x + 2} \right)}^2}.2\left( {x + 2} \right)}} = {{8x\left( {x + 2} \right)} \over {2{{\left( {x + 2} \right)}^3}}} \cr & {3 \over {2x + 4}} = {3 \over {2\left( {x + 2} \right)}} = {{3{{\left( {x + 2} \right)}^2}} \over {2\left( {x + 2} \right){{\left( {x + 2} \right)}^2}}} = {{3{{\left( {x + 2} \right)}^2}} \over {2{{\left( {x + 2} \right)}^3}}} \cr} \)
Câu 15: Cho đa thức B \( = 2{x^3} + 3{x^2} – 29x + 30\) và hai phân thức
\({x \over {2{x^2} + 7x – 15}}\), \({{x + 2} \over {{x^2} + 3x – 10}}\)
a. Chia đa thức B lần lượt cho các mẫu thức của hai phân thức đã cho.
b. Quy đồng mẫu thức của hai phân thức đã cho.


b. MTC = \(2{x^3} + 3{x^2} – 29x + 30\)
\(\eqalign{ & {x \over {2{x^2} + 7x – 15}} = {{x\left( {x – 2} \right)} \over {\left( {2{x^2} + 7x – 15} \right)\left( {x – 2} \right)}} = {{{x^2} – 2x} \over {2{x^3} + 3{x^2} – 29x + 30}} \cr & {{x + 2} \over {{x^2} + 3x – 10}} = {{\left( {x + 2} \right)\left( {2x – 3} \right)} \over {\left( {{x^2} + 3x – 10} \right)\left( {2x – 3} \right)}} = {{\left( {x + 2} \right)\left( {x – 3} \right)} \over {2{x^3} + 3{x^2} – 29x + 30}} \cr} \)
Câu 16: Cho hai phân thức \({1 \over {{x^2} + 7x – 15}}\) và \({2 \over {{x^2} – 2x – 3}}\)
Chứng tỏ rằng có thể chọn đa thức \({x^3} – 7{x^2} + 7x + 15\) làm mẫu thức chung để quy đồng mẫu thức hai phân thức đã cho. Hãy quy đồng mẫu thức.

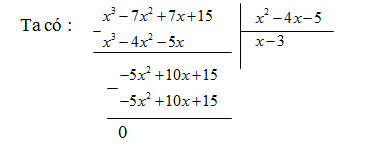
Suy ra: \({x^3} – 7{x^2} + 7x + 15 = \left( {{x^2} – 4x – 5} \right)\left( {x – 3} \right)\)

Suy ra: \({x^3} – 7{x^2} + 7x + 15 = \left( {{x^2} – 2x – 3} \right)\left( {x – 5} \right)\)
\(\eqalign{ & {1 \over {{x^2} – 4x – 5}} = {{1.\left( {x – 3} \right)} \over {\left( {{x^2} – 4x – 5} \right).\left( {x – 3} \right)}} = {{x – 3} \over {{x^3} – 7{x^2} + 7x + 15}} \cr & {2 \over {{x^2} – 2x – 3}} = {{2.\left( {x – 5} \right)} \over {\left( {{x^2} – 2x – 3} \right)\left( {x – 5} \right)}} = {{2\left( {x – 5} \right)} \over {{x^3} – 7{x^2} + 7x + 15}} \cr} \)

