Câu 9: Cho tam giác nhọn ABC. Vẽ đường tròn (O) có đường kính BC, nó cắt các cạnh AB, AC theo thứ tự ở D, E.
a) Chứng minh rằng \(CD \bot AB,BE \bot AC.\)
b) Gọi K là giao điểm của BE và CD. Chứng minh rằng AK vuông góc với BC.

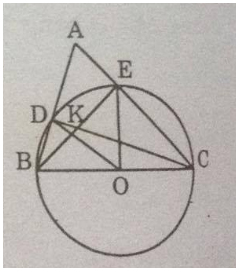
a) Tam giác BCD nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại D.
Suy ra: \(CD \bot AB\)
Tam giác BCE nội tiếp trong đường tròn (O) có BC là đường kính nên vuông tại E.
Suy ra: \(BE \bot AC\)
b) K là giao điểm của hai đường cao CD và BE nên K là trực tâm của tam giác ABC.
Suy ra: \(AK \bot BC\)
Câu 10: Cho tam giác đều ABC cạnh bằng 3cm. Bán kính của đường tròn ngoại tiếp tam giác ABC bằng
\((A)\,2\sqrt 3 \,cm;\)
\((B)\, 2cm;\)
\((C)\,\sqrt 3 \,cm;\)
\((D)\,\sqrt 2 \,cm;\)
Hãy chọn câu trả lời đúng.

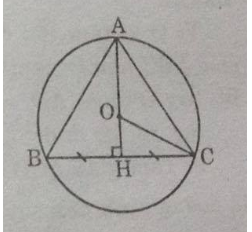
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O là giao điểm của ba đường trung trực trong tam giác ABC.
Advertisements (Quảng cáo)
Kẻ \(AH \bot BC.\), ta có: \(O \in AH\).
Trong tam giác vuông ABH, ta có:
\(AH = AB.\sin \widehat C = 3.\sin 60^\circ = {{3\sqrt 3 } \over 2}\)
Vì tam giác ABC đều nên AH là đường cao cũng đồng thời là trung tuyến nên:
\(OA = {2 \over 3}AH = {2 \over 3}.{{3\sqrt 3 } \over 2} = \sqrt 3 \)
Vậy chọn đáp án C.
Câu 11:
a) Chứng minh rằng bốn đỉnh của hình vuông cùng nằm trên một đường tròn. Hãy chỉ ra vị trí của tâm đường tròn đó.
b) Tính bán kính của đường tròn đó, biết cạnh của hình vuông bằng 2dm.

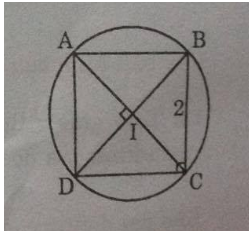
a) Gọi I là giao điểm của hai đường chéo AC và BD
Ta có:
Advertisements (Quảng cáo)
IA = IB = IC = ID (tính chất của hình vuông)
Vậy bốn điểm A, B, C, D cùng nằm trên một đường tròn. Tâm của đường tròn là I.
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} = {2^2} + {2^2} = 8\)
Suy ra: \(AC = \,2\sqrt 2 \,(cm)\)
Vậy \(R = IA = {{AC} \over 2} = {{2\sqrt 2 } \over 2} = \sqrt 2 \,(cm)\)
Câu 12
Cho tam giác ABC cân tại A, nội tiếp đường tròn (O). Đường cao AH cắt đường tròn ở D.
a) Vì sao AD là đường kính của đường tròn (O)?
b) Tính số đo góc ACD.
c) Cho BC = 24cm, AC = 20cm. Tính đường cao AH và bán kính đường tròn (O).

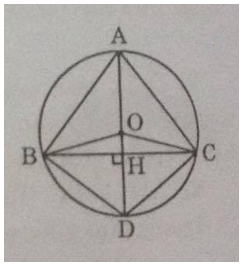
Tam giác ABC cân tại A nên AH là đường cao đồng thời cũng là đường trung trực của BC.
Vì O là tâm của đường tròn ngoại tiếp tam giác ABC nên O nằm trên đường trung trực của BC hay O thuộc AD.
Suy ra AD là đường kính của (O).
b) Tam giác ACD nội tiếp trong (O) có AD là đường kính nên suy ra \(\widehat {ACD} = 90^\circ \)
c) Ta có:
\(\eqalign{
& AH \bot BC \cr
& \Rightarrow HB = HC = {{BC} \over 2} = {{24} \over 2} = 12\,(cm) \cr} \)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH ta có:
\(A{C^2} = A{H^2} + H{C^2}\)
Suy ra:
\(\eqalign{
& A{H^2} = A{C^2} – H{C^2} \cr
& = {20^2} – {12^2} = 400 – 144 = 256 \cr} \)
\(AH = 16\,(cm)\)
Tam giác ACD vuông tại C theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& A{C^2} = AH.AD \cr
& \Rightarrow AD = {{A{C^2}} \over {AH}} = {{{{20}^2}} \over {16}} = 25\,(cm) \cr} \)
Vậy bán kính của đường tròn (O) là :
\(R = {{AD} \over 2} = {{25} \over 2} = 12,5\,(cm)\)

