Câu 7: Cho hàm số \(y = 0,1{x^2}\)
a) Vẽ đồ thị của hàm số.
b) Các điểm sau có thuộc đồ thị hay không: A(3; 0,9), B(-5; 2,5), C(-10, 1)?
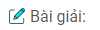
a) Vẽ đồ thị hàm số \(y = 0,1{x^2}\)
|
x |
-5 |
-2 |
0 |
2 |
5 |
| \(y = 0,1{x^2}\) |
2,5 |
0,4 |
0 |
0,4 |
2,5 |
b) Thay hoành độ điểm A vào phương trình hàm số:
\(y = 0,{1.3^2} = 0,9 = {y_A}\)
Vậy điểm A (3; 0,9) thuộc đồ thị hàm số.
Thay hoành độ điểm B vào phương trình hàm số:
\(y = 0,1{\left( { – 5} \right)^2} = 0,1.25 = 2,5 = {y_B}\)
Vậy điểm B (-5; 2,5) thuộc đồ thị hàm số.
Thay hoành độ điểm C vào phương trình hàm số:
\(y = 0,1{\left( { – 10} \right)^2} = 0,1.100 = 10 \ne {y_C}\).
Vậy điểm C (-10; 10) không thuộc đồ thị hàm số.
Advertisements (Quảng cáo)
Câu 8: Cho hàm số \(y = a{x^2}\). Xác định hệ số a trong các trường hợp sau:
a) Đồ thị của nó đi qua điểm A(3; 12);
b) Đồ thị của nó đi qua điểm B(-2; 3).
a) Đồ thị hàm số \(y = a{x^2}\) đi qua điểm A (3; 12) nên tọa độ của A nghiệm đúng phương trình hàm số.
Ta có: \(12 = a{.3^2} \Leftrightarrow a = {{12} \over 9} = {4 \over 3}\)
Hàm số đã cho: \(y = {4 \over 3}{x^2}\)
b) Đồ thị hàm số \(y = a{x^2}\) đi qua điểm B (-2; 3) nên tọa độ của điểm B nghiệm đúng phương trình hàm số: \(3 = a{\left( { – 2} \right)^2} \Leftrightarrow a = {3 \over 4}\)
Hàm số đã cho: \(y = {3 \over 4}{x^2}\)
Advertisements (Quảng cáo)
Câu 9: Cho hàm số \(y = 0,2{x^2}\)
a) Biết rằng điểm A(-2; b) thuộc đồ thị, hãy tính b. Điểm A’(2; b) có thuộc đồ thị của hàm số không? Vì sao?
b) Biết rằng điểm C(c; 6) thuộc đồ thị, hãy tính c. Điểm D(c; -6) có thuộc đồ thị không? Vì sao?
a) Điểm A (2; b) thuộc đồ thị hàm số \(y = 0,2{x^2}\) nên tọa độ của điểm A nghiệm đúng phương trình hàm số
Ta có: \(b = 0,{2.2^2} = 0,8\)
Điểm A’ (2; b) đối xứng với điểm A (-2; b) qua trục tung mà điểm A (2; b) thuộc đồ thị hàm số \(y = 0,2{x^2}\) nên điểm A’(2; b) thuộc đồ thị hàm số \(y = 0,2{x^2}\).
b) Điểm C (c; 6) thuộc đồ thị hàm số \(y = 0,2{x^2}\) nên tọa độ của điểm C nghiệm đúng phương trình hàm số:
Ta có: \(6 = 0,2.{c^2} \Leftrightarrow {c^2} = {6 \over {0,2}} = 30 \Rightarrow c = \pm \sqrt {30} \)
Điểm D (c; -6) đối xứng với điểm C (c; 6) qua trục hoành mà đồ thị hàm số \(y = 0,2{x^2}\) gồm 2 nhánh đối xứng qua trục tung nên C (c; 6) thuộc đồ thị hàm số thì điểm D (c; -6) không thuộc đồ thị hàm số.
Câu 10
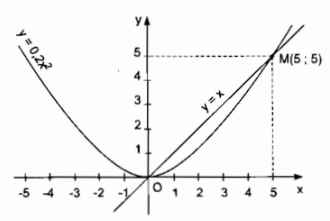
Cho hai hàm số \(y = 0,2{x^2}\) và \(y = x\)
a) Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
b) Tìm tọa độ của các giao điểm của hai đồ thị.
a) Vẽ đồ thị hàm số \(y = 0,2{x^2}\)
|
x |
-5 |
-2 |
0 |
2 |
5 |
| \(y = 0,2{x^2}\) |
5 |
0,8 |
0 |
0,8 |
5 |
Vẽ đồ thị hàm số \(y = x\). Đồ thị đi qua O (0; 0)
Cho \(x = 5 \Rightarrow y = 5\) M(5; 5)