Câu 39: Trên đường tròn tâm O có một cung AB và S là điểm chính giữa của cung đó. Trên dây AB lấy hai điểm E và H. Các đường thẳng SH và SE cắt đường tròn theo thứ tự tại C và D. Chứng minh EHCD là một tứ giác nội tiếp.
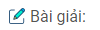
S là điểm chính giữa của cung \(\overparen{AB}\).
\( \Rightarrow \) \(\overparen{SA}\) = \(\overparen{SB}\) (1)
\(\widehat {DEB} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{AS}\)) tính chất góc có đỉnh ở bên trong đường tròn) (2)
\(\widehat {DCS} = {1 \over 2}\) sđ \(\overparen{DAS}\) (tính chất góc nội tiếp) hay \(\widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DA}\) + sđ \(\overparen{SA}\)) (3)
Từ (1) và (2) suy ra: \(\widehat {DEB} + \widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{AS}\) + sđ \(\overparen{DA}\) + sđ \(\overparen{SA}\) (4)
Từ (1) và (4) suy ra: \(\widehat {DEB} + \widehat {DCS} = {1 \over 2}\) (sđ \(\overparen{DCB}\) + sđ \(\overparen{BS}\) + sđ \(\overparen{SA}\) + sđ \(\overparen{DA}\) \( = {{360^\circ } \over 2} = 180^\circ \)
Hay \(\widehat {DEH} + \widehat {DCH} = 180^\circ \)
Vậy: tứ giác EHCD nội tiếp được trong một đường tròn.
Câu 40: Cho tam giác ABC. Các đường phân giác trong của \(\widehat B\) và \(\widehat C\) cắt nhau tại S, các đường phân giác ngoài của \(\widehat B\) và \(\widehat C\) cắt nhau tại E. Chứng minh BSCE là một tứ giác nội tiếp.
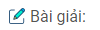
Advertisements (Quảng cáo)
BS ⊥ BE (tính chất hai góc kề bù)
\( \Rightarrow \widehat {SBE} = 90^\circ \)
CS ⊥ CE (tính chất hai góc kề bù)
\( \Rightarrow \widehat {SCE} = 90^\circ \)
Xét tứ giác BSCE ta có: \(\widehat {SBE} + \widehat {SCE} = 180^\circ \)
Vậy tứ giác BSCE nội tiếp.
Câu 41: Cho tam giác cân ABC có đáy BC và \(\widehat A = {20^0}\). Trên nửa mặt phẳng bờ AB không chứa điểm C lấy điểm D sao cho DA = DB và \(\widehat {DAB} = {40^0}\). Gọi E là giao điểm của AB và CD.
a) Chứng minh ABCD là tứ giác nội tiếp
b) Tính \(\widehat {AED}\)
Advertisements (Quảng cáo)
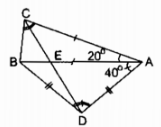
a) ∆ABC cân tại A (gt).
\( \Rightarrow \widehat {ACB} = \widehat {ABC}\) (tính chất tam giác cân)
\( \Rightarrow \widehat {ACB} = {{180^\circ – \widehat A} \over 2} = {{180^\circ – 20^\circ } \over 2} = 80^\circ \)
∆DAB cân tại D.
\( \Rightarrow \widehat {DBA} = \widehat {DAB}\) (tính chất tam giác cân) mà \(\widehat {DAB} = 40^\circ \) (gt) \( \Rightarrow \widehat {DBA} = 40^\circ \)
\(\widehat {ADB} = 180^\circ – (\widehat {DAB} + \widehat {DBA}) = 180^\circ – (40^\circ + 40^\circ ) = 100^\circ \)
Trong tứ giác ACBD ta có: \(\widehat {ACB} + \widehat {ADB} = 80^\circ + 100^\circ = 180^\circ \)
Vậy: Tứ giác ACBD nội tiếp.
b) Tứ giác ACBD nội tiếp
\(\widehat {BAC} = {1 \over 2}\) sđ \(\overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\)\( = 2\widehat {BAC} = 2.20^\circ = 40^\circ \)
\(\widehat {DBA} = {1 \over 2}\) sđ \(\overparen{AD}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AD}\) \( = 2\widehat {DBA} = 2.40^\circ = 80^\circ \)
\(\widehat {AED}\) là góc có đỉnh ở trong đường tròn ngoại tiếp tứ giác ACBD
\(\widehat {AED} = {1 \over 2}\)(sđ \(\overparen{BC}\) + sđ \(\overparen{AD}\)) \( = {{40^\circ + 80^\circ } \over 2} = 60^\circ \)

