Câu 21: Cho tam giác ABC nội tiếp trong đường tròn tâm O, biết \(\widehat A = {32^0}\), \(\widehat B = {84^0}\). Lấy các điểm D, E, F thuộc đường tròn tâm O sao cho AD = AB, BE = BC, CF = CA. Hãy tính các góc của tam giác DEF.
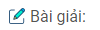
\(\widehat A = {1 \over 2}\) sđ \(\overparen{BC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{BC}\) \( = 2\widehat A = {2.32^0} = {64^0}\)
BC = BE (gt)
\( \Rightarrow \) sđ \(\overparen{BC}\) = sđ \(\overparen{BE}\) = 640
\(\widehat B = {1 \over 2}\) sđ \(\overparen{AC}\) (tính chất góc nội tiếp)
\( \Rightarrow \) sđ \(\overparen{AC}\) \( = 2\widehat B = {2.84^0} = {168^0}\)
AC = CF (gt)
\( \Rightarrow \) sđ \(\overparen{CF}\) = sđ \(\overparen{AC}\) = 1680
sđ \(\overparen{AC}\) + sđ \(\overparen{AF}\) + sđ \(\overparen{CF}\) = 3600
\( \Rightarrow \) sđ \(\overparen{AF}\) \( = {360^0} – \) sđ \(\overparen{AC}\) – sđ \(\overparen{CF}\) = 3600 – 1680. 2 = 240
Trong ∆ABC ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\)
\( \Rightarrow \widehat {ACB} = {180^0} – \left( {\widehat A + \widehat B} \right)\)
= \({180^0} – \left( {{{32}^0} + {{84}^0}} \right) = {64^0}\)
sđ \(\widehat {ACB} = {1 \over 2}\) sđ \(\overparen{AB}\)
\( \Rightarrow \) sđ \(\overparen{AB}\) \( = 2\widehat {ACB} = {2.64^0} = {128^0}\)
Advertisements (Quảng cáo)
AD = AB (gt)
\( \Rightarrow \) sđ \(\overparen{AD}\) = sđ \(\overparen{AB}\) = 1280
\(\widehat {FED} = {1 \over 2}\) sđ \(\overparen{DF}\) \( = {1 \over 2}\) ( sđ \(\overparen{AD}\) + sđ \(\overparen{AF}\))
= \({1 \over 2}.\left( {{{128}^0} + {{24}^0}} \right) = {76^0}\)
\(\widehat {EDF} = {1 \over 2}\) sđ \(\overparen{EF}\) = \({1 \over 2}\) ( sđ \(\overparen{AB}\) – sđ \(\overparen{AF}\) – sđ \(\overparen{BE}\)
= \({1 \over 2}.\left( {{{128}^0} – {{24}^0} – {{64}^0}} \right) = {20^0}\)
\(\widehat {DFE} = {180^0} – \left( {\widehat {FED} + \widehat {EDF}} \right)\)
= \({180^0} – \left( {{{76}^0} + {{20}^0}} \right) = {84^0}\).
Câu 22: Vẽ một tam giác vuông biết cạnh huyền là 4cm và đường cao ứng với cạnh huyền là 1,5cm.
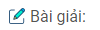
Cách vẽ:
Advertisements (Quảng cáo)
– Vẽ đoạn BC = 4cm.
– Vẽ nửa đường tròn đường kính BC
– Vẽ đường thẳng xy nằm trên nửa mặt phẳng chứa nửa đường tròn và xy // BC, cách BC một khoảng bằng 1,5cm.
– Đường thẳng xy cắt nửa đường tròn đường kính BC tại A và A’. Nối AB, AC, A’B, A’C ta có ∆ABC hoặc ∆A’BC cần vẽ.
Thật vậy: xy cách BC một khoảng 1,5m < \({{BC} \over 2} = 2\) cm nên đường thẳng xy cắt nửa đường tròn đường kính BC.
Ta lại có ∆ABC nội tiếp trong nửa đường tròn đường kính BC nên \(\widehat {BAC} = {90^0}\)
Có \(AH \bot BC\) và AH = 1,5 cm.
Câu 23: Cho tam giác cân ABC (AB = AC) nội tiếp đường tròn tâm O. Các đường phân giác của hai góc B và C cắt nhau ở E và cắt đường tròn lần lướt ở F và D. Chứng minh rằng tứ giác EBAF là một hình thoi.
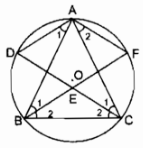
∆ABC cân tại A
\( \Rightarrow \widehat {ABC} = \widehat {ACB}\) (tính chất tam giác cân)
BF là tia phân giác của \(\widehat {ABC}\) (gt)
CD là tia phân giác của \(\widehat {ACB}\) (gt)
Suy ra: \(\widehat {{B_1}} = \widehat {{B_2}} = \widehat {{C_1}} = \widehat {{C_2}}\)
Suy ra: \(\overparen{AD}\)=\(\overparen{DB}\)=\(\overparen{AF}\)=\(\overparen{FC}\)
\(\widehat {{A_1}} = \widehat {{B_1}}\) (hai góc nội tiếp chắn 2 cung bằng nhau)
\( \Rightarrow AD//BF\) (vì có cặp góc so le trong bằng nhau)
Hay AD // EF (1)
\(\widehat {{A_2}} = \widehat {{C_1}}\) (hai góc nội tiếp chắn 2 cung bằng nhau)
\( \Rightarrow \) AF // CD (vì có cặp góc ở vị trí so le trong bằng nhau)
Hay AF // ED (2)
\(\overparen{AD}\) = \(\overparen{AF}\) (chứng minh trên)
\( \Rightarrow AD = AF\) (3)
Từ (1), (2) và (3) suy ra: Tứ giác ADEF là hình thoi

