Câu 80: Hãy tính sinα và tgα, nếu
a) \(\cos \alpha = {5 \over {13}}\);
b) \(\cos \alpha = {{15} \over {17}}\);
c) \(\cos \alpha = 0,6.\)

a) \(cos \alpha = {5 \over {13}}\)
* Ta có:
\({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Suy ra:
\(\eqalign{
& {\sin ^2}\alpha = 1 – {\cos ^2}\alpha = 1 – {\left( {{5 \over {13}}} \right)^2} \cr
& = 1 – {{25} \over {169}} = {{144} \over {169}} \cr} \)
Vì \(\sin \alpha > 0\) nên \(\sin \alpha = \sqrt {{{144} \over {169}}} = {{12} \over {13}}\)
* \(tg\alpha = {{\sin \alpha } \over {\cos \alpha }} = {{{{12} \over {13}}} \over {{5 \over {13}}}} = {{12} \over {13}}.{{13} \over 5} = {{12} \over 5}\)
b) \(\cos \alpha = {{15} \over {17}}\)
* Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\)
Suy ra:
\(\eqalign{
& {\sin ^2}\alpha = 1 – {\cos ^2}\alpha = 1 – {\left( {{{15} \over {17}}} \right)^2} \cr
& = 1 – {{225} \over {289}} = {{64} \over {289}} \cr} \)
Vì \(\sin \alpha > 0\) nên \(\sin \alpha = \sqrt {{{64} \over {289}}} = {8 \over {17}}\)
* \(tg\alpha {{\sin \alpha } \over {\cos \alpha }} = {{{8 \over {17}}} \over {{{15} \over {17}}}} = {8 \over {17}}.{{17} \over {15}} = {8 \over {15}}\)
c) \(\cos \alpha = 0,6\)
* Ta có: \({\sin ^2}\alpha + {\cos ^2}\alpha = 1.\)
Suy ra: \({\sin ^2}\alpha = 1 – {\cos ^2}\alpha \)
\( = 1 – {(0,6)^2} = 1 – 0,36 = 0,64\)
Vì \(\sin \alpha > 0\) nên \(\sin \alpha = \sqrt {0,64} = 0,8\)
* \(tg\alpha = {{\sin \alpha } \over {\cos \alpha }} = {{0,8} \over {0,6}} = {8 \over 6} = {4 \over 3}\)
Câu 81: Hãy đơn giản các biểu thức
a) \(1 – {\sin ^2}\alpha \);
b) \((1 – \cos \alpha )(1 + \cos \alpha )\);
Advertisements (Quảng cáo)
c) \(1 + {\sin ^2}\alpha + {\cos ^2}\alpha \);
d) \(\sin \alpha – \sin \alpha .{\cos ^2}\alpha \);
e) \({\sin ^4}\alpha + {\cos ^4}\alpha + 2.{\sin ^2}\alpha .{\cos ^2}\alpha \);
g) \(t{g^2}\alpha – {\sin ^2}\alpha .t{g^2}\alpha \);
h) \({\cos ^2}\alpha + t{g^2}\alpha .c{\rm{o}}{{\rm{s}}^2}\alpha \);
i) \(t{g^2}\alpha (2.{\cos ^2}\alpha + {\sin ^2}\alpha – 1).\)

a) \(1 – {\sin ^2}\alpha = ({\sin ^2}\alpha + {\cos ^2}\alpha ) – {\sin ^2}\alpha \)
\( = {\sin ^2}\alpha + {\cos ^2}\alpha – {\sin ^2}\alpha = {\cos ^2}\alpha \)
\(\eqalign{
& b)\,(1 – \cos \alpha )(1 + \cos \alpha ) = 1 – {\cos ^2}\alpha \cr
& = ({\sin ^2}\alpha + {\cos ^2}\alpha ) – {\cos ^2}\alpha \cr} \)
\( = {\sin ^2}\alpha + {\cos ^2}\alpha – {\cos ^2}\alpha = {\sin ^2}\alpha \)
\(\eqalign{
& c)\,1 + {\sin ^2}\alpha + {\cos ^2}\alpha \cr
& = 1 + ({\sin ^2}\alpha + {\cos ^2}\alpha ) = 1 + 1 = 2 \cr} \)
d) \(\sin \alpha – \sin \alpha .{\cos ^2}\alpha = \sin \alpha (1 – {\cos ^2}\alpha )\)
\( = \sin \alpha \left[ {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) – {{\cos }^2}\alpha } \right]\)
\( = \sin \alpha ({\sin ^2}\alpha + {\cos ^2}\alpha – {\cos ^2}\alpha )\)
\( = \sin \alpha .{\sin ^2}\alpha = {\sin ^3}\alpha \)
\(\eqalign{
& e)\,{\sin ^4}\alpha + {\cos ^4}\alpha + 2.{\sin ^2}\alpha .{\cos ^2}\alpha \cr
& = {({\sin ^2}\alpha + {\cos ^2}\alpha )^2} = {1^2} = 1 \cr} \)
Advertisements (Quảng cáo)
g) \(t{g^2}\alpha – {\sin ^2}\alpha .t{g^2}\alpha \)\( = t{g^2}\alpha (1 – {\sin ^2}\alpha )\)
\( = t{g^2}\left[ {\left( {{{\sin }^2}\alpha + {{\cos }^2}\alpha } \right) – {{\sin }^2}\alpha } \right]\)
\( = t{g^2}\alpha .{\cos ^2}\alpha = {{{{\sin }^2}\alpha } \over {{{\cos }^2}\alpha }}.{\cos ^2}\alpha = {\sin ^2}\alpha \)
\(\eqalign{
& h)\,{\cos ^2}\alpha + t{g^2}\alpha .c{\rm{o}}{{\rm{s}}^2}\alpha \cr
& = c{\rm{o}}{{\rm{s}}^2}\alpha + {{{{\sin }^2}\alpha } \over {c{\rm{o}}{{\rm{s}}^2}\alpha }}.c{\rm{o}}{{\rm{s}}^2}\alpha \cr
& = c{\rm{o}}{{\rm{s}}^2}\alpha + {\sin ^2}\alpha = 1 \cr} \)
\(\eqalign{
& i)\,t{g^2}\alpha (2.{\cos ^2}\alpha + {\sin ^2}\alpha – 1) \cr
& = t{g^2}\alpha .\left[ {{{\cos }^2}\alpha + \left( {{{\cos }^2}\alpha + {{\sin }^2}\alpha } \right) – 1} \right] \cr} \)
\( = t{g^2}\alpha .({\cos ^2}\alpha + 1 – 1) = t{g^2}\alpha .{\cos ^2}\alpha \)
\( = {{{{\sin }^2}\alpha } \over {{{\cos }^2}\alpha }}.{\cos ^2}\alpha = {\sin ^2}\alpha \)
Câu 82: Trong một tam giác với các cạnh có độ dài 6,7,9, kẻ đường cao đến cạnh lớn nhất. Hãy tìm độ dài đường cao này và các đoạn thẳng mà nó định ra trên cạnh lớn nhất đó.

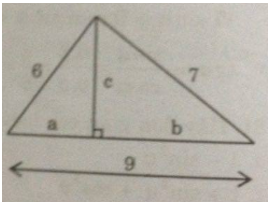
Gọi độ dài đường cao là c, hình chiếu cả hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.
Ta có: a < b (6 < 7)
Theo định lí Pi-ta-go, ta có:
\({c^2} = {6^2} – a\)
\({c^2} = {7^2} – {b^2}\)
Suy ra: \(36 – {a^2} = 49 – {b^2}\)
\( \Leftrightarrow {b^2} – {a^2} = 49 – 36\)
\( \Leftrightarrow (b + a)(b – a) = 13\,(*)\)
Mà x +y = 9 nên:
\(\eqalign{
& 9.(b – a) = 13 \Leftrightarrow b – a = {{13} \over 9} \cr
& \Rightarrow b = a + {{13} \over 9} \cr} \)
Thay vào (*), ta có:
\(\left[ {\left( {a + {{13} \over 9}} \right) + a} \right].{{13} \over 9} = 13 \Leftrightarrow 2a + {{13} \over 9} = {{13} \over {{{13} \over 9}}}\)
\(\eqalign{
& \Leftrightarrow 2a + {{13} \over 9} = 13.{9 \over {13}} \Leftrightarrow 2a + {{13} \over 9} = 9 \cr
& \Leftrightarrow a = {{9 – {{13} \over 9}} \over 2} = {{34} \over 9} \cr} \)
Suy ra: \(b = 9 – a = 9 – {{34} \over 9} = {{47} \over 9}\)
\(c = \sqrt {49 – {{\left( {{{47} \over 9}} \right)}^2}} \approx 4,7\)
Câu 83: Hãy tìm độ dài cạnh đáy của một tam giác cân, nếu đường cao kẻ xuống đáy có độ dài là 5 và đường cao kẻ xuống cạnh bên có độ dài là 6.

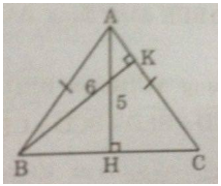
Giả sử ∆ABC cân tại A có \(AH \bot BC,AH = 5,BK \bot AC,BK = 6.\)
Ta có: \(HB = HC = {1 \over 2}BC\) (tính chất tam giác cân)
\(\eqalign{
& {S_{ABC}} = {1 \over 2}AH.BC = {1 \over 2}BK.AC \cr
& = {1 \over 2}.5.BC = {1 \over 2}.6.AC \cr} \)
Suy ra: \(5BC = 6AC \Rightarrow BC = {6 \over 5}AC\,(1)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACH, ta có:
\(A{C^2} = A{H^2} + H{C^2} = {5^2} + {\left( {{{BC} \over 2}} \right)^2} = 25 + {{B{C^2}} \over 4}\,(2)\)
Từ (1) và (2) suy ra:
\(A{C^2} = 25 + {{{{36A{C^2}} \over {25}}} \over 4} = {{2500} \over {100}} + {{36A{C^2}} \over {100}}\)
Suy ra:
\(100A{C^2} = 2500 + 36A{C^2}\)
\( \Leftrightarrow 64A{C^2} = 2500 \Leftrightarrow 8AC = 50 \Rightarrow AC = 6,25\)
Vậy \(BC = {6 \over 5}.6,25 = 7,5.\)

