Câu 43: Cho hình
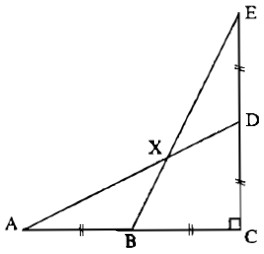
Biết:
\(\widehat {ACE} = 90^\circ ,AB = BC = CD = DE = 2cm.\)
Hãy tính:
a) AD, BE;
b) \(\widehat {DAC}\);
c) \(\widehat {BXD}\).

a) Ta có:
\(AC = AB + BC = 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông ACD, ta có:
\(A{D^2} = A{C^2} + C{D^2} = {4^2} + {2^2} = 16 + 4 = 20\)
\( \Rightarrow AD = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
Mặt khác: \(CE = CD + DE = 2 + 2 = 4\left( {cm} \right)\)
Áp dụng định lí Pi-ta-go vào tam giác vuông BEC, ta có:
\(B{E^2} = B{C^2} + C{E^2} = {2^2} + {4^2} = 4 + 16 = 20\)
\( \Rightarrow BE = \sqrt {20} = 2\sqrt 5 \left( {cm} \right)\)
b) Tam giác ACD vuông tại C nên ta có: \(tg\widehat {DAC} = {{CD} \over {AC}} = {2 \over 4} = {1 \over 2}\)
Suy ra: \(\widehat {DAC} \approx 26^\circ 34’\)
Ta có: \(\widehat {CDA} = 90^\circ – \widehat {CAD} \approx 90^\circ – 26^\circ 34′ = 63^\circ 26’\)
Advertisements (Quảng cáo)
Trong tứ giác BCDX, ta có:
\(\widehat {BXD} = 360^\circ – (\widehat C + \widehat {CDA} + \widehat {CBE})\)
\( = 360^\circ – (90^\circ + 63^\circ 26′ + 63^\circ 26′) = 143^\circ 8′.\)
Câu 44: Đoạn thẳng LN vuông góc với đoạn thẳng AB tại trung điểm N của AB; M là một điểm của đoạn thẳng LN và khác với L,N. Hãy so sánh các góc \(\widehat {LAN}\) và \(\widehat {MBN}\).

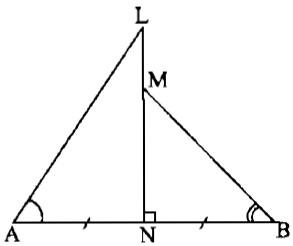
Tam giác ALN vuông tại N nên ta có:
\(tg\widehat {LAN} = {{NL} \over {AN}}\) (1)
Tam giác BNM vuông tại N nên ta có:
\(tg\widehat {MBN} = {{NM} \over {NB}}\) (2)
Mặt khác: AN = NB (gt) (3)
NL > NM (4)
Từ (1), (2), (3) và (4) suy ra: \(tg\widehat {MBN} < tg\widehat {LAN}\)
Suy ra: \(\widehat {MBN} < tg\widehat {LAN}\) ( vì \(\alpha \) tăng thì tg\(\alpha \) tăng).
Advertisements (Quảng cáo)
Sachbaiatp.com
Câu 45: Không dùng bảng lượng giác và máy tính bỏ túi, hãy so sánh
a) \(\sin 25^\circ \) và \(\sin 70^\circ \); b) \(\cos 40^\circ \) và \(\cos 75^\circ \) ;
c) \(\sin 38^\circ \) và \(\cos 38^\circ \) ; d) \(\sin 50^\circ \) và \(\cos 50^\circ \).

a) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha\) tăng thì sin\(\alpha\ tăng
Ta có: \(25^\circ < 75^\circ \), suy ra: \(\sin 25^\circ < \sin 75^\circ \)
b) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha\) tăng thì sin\(\alpha\) giảm
Ta có: \(40^\circ < 75^\circ \), suy ra: \({\rm{cos40}}^\circ {\rm{ > cos}}75^\circ \)
c) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha\) tăng thì sin\(\alpha\) tăng
Ta có: \(38^\circ + 52^\circ = 90^\circ \), suy ra: \(\cos 38^\circ = \sin 52^\circ \)
Vì \(38^\circ < 52^\circ \) nên \(\sin 38^\circ < \sin 52^\circ \) hay \(\sin 38^\circ < \cos 38^\circ \)
d) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha\) tăng thì cos\(\alpha\) giảm
Ta có: \(40^\circ + 50^\circ = 90^\circ ,\) suy ra: \(\sin 50^\circ = \cos 40^\circ \)
Vì \(40^\circ < 50^\circ \) nên \(\cos 40^\circ > \cos 50^\circ \) hay \(\sin 50^\circ > \cos 50^\circ \)
Câu 46: Không dùng bảng lượng giác hoặc máy tính bỏ túi,hãy so sánh
a) \(tg50^\circ 28’\) và \(tg63^\circ \); b) \(\cot g14^\circ \) và \(\cot g35^\circ 12’\);
c) \(tg27^\circ \) và \(\cot g27^\circ \); d) \(tg65^\circ \) và \(\cot g65^\circ \).

a) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha \) tăng thì tg\(\alpha \) tăng
Ta có: \(50^\circ 28′ < 63^\circ ,\) suy ra: \(tg50^\circ 28′ < tg63^\circ \)
b) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha \) tăng thì cotg\(\alpha \) giảm
Ta có: \(14^\circ < 35^\circ 12′,\) suy ra: cotg14°> cotg35°12’
c) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha \) tăng thì tg\(\alpha \) tăng
Ta có: \(27^\circ + 63^\circ = 90^\circ ,\) suy ra: \(\cot g27^\circ = tg63^\circ \)
Vì \(27^\circ < 63^\circ \) nên \(tg27^\circ < tg63^\circ \) hay \(tg27^\circ < \cot g27^\circ \)
d) Với \(0^\circ < \alpha < 90^\circ \) ta có \(\alpha \) tăng thì cotg\(\alpha \) giảm
Ta có: \(65^\circ + 25^\circ = 90^\circ \) nên tg65° =cotg25°
Vì 25 < 65 nên cotg25 > cotg65 hay tg65° > cotg65°.

