Câu 13: Cho hai đoạn thẳng có độ dài là a và b. Dựng các đoạn thẳng có độ dài tương ứng bằng
a) \(\sqrt {{a^2} + {b^2}}\) b) \(\sqrt {{a^2} – {b^2}} \,,\,\left( {a > 0} \right)\)

a) \(\sqrt {{a^2} + {b^2}}\)
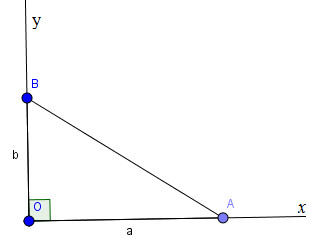
* Cách dựng (hình a):
− Dựng góc vuông xOy.
− Trên tia Ox, dựng đoạn OA = a.
− Trên tia Oy, dựng đoạn OB = b.
− Nối AB ta có đoạn \(AB = \sqrt {{a^2} + {b^2}} \) cần dựng.
* Chứng minh:
Áp dụng định lý Pi-ta-go vào tam giác vuông AOB, ta có:
\(A{B^2} = O{A^2} + O{B^2} = {a^2} + {b^2}\)
Suy ra: \(AB = \sqrt {{a^2} + {b^2}} \)
b) \(\sqrt {{a^2} – {b^2}} \,,\,\left( {a > 0} \right)\)
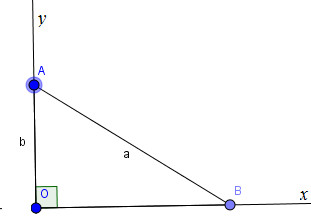
* Cách dựng (hình b):
− Dựng góc vuông xOy.
− Trên tia Ox, dựng đoạn OA = b.
− Dựng cung tròn tâm A, bán kính bằng a cắt Oy tại B.
Advertisements (Quảng cáo)
Ta có đoạn \(OB = \sqrt {{a^2} – {b^2}} (a > b)\) cần dựng.
* Chứng minh;
Áp dụng định lí Pi-ta-go vào tam giác vuông AOB, ta có:
\(A{B^2} = O{A^2} + O{B^2} \Rightarrow O{B^2} = A{B^2} – O{A^2} = {a^2} – {b^2}\)
Suy ra: \(OB = \sqrt {{a^2} – {b^2}} \)
Câu 14: Cho hai đoạn thẳng có độ dài là a và b. Dựng đoạn thẳng \(\sqrt {ab} \) như thế nào?

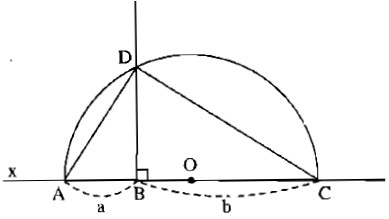
* Cách dựng:
− Dựng đường thẳng t.
− Trên đường thẳng t dựng liên tiếp hai đoạn thẳng AB = a, BC = b.
− Dựng nửa đường tròn tâm O đường kính AC.
Advertisements (Quảng cáo)
− Từ B dựng đường thẳng vuông góc với AC cắt nửa đường tròn tâm O tại D.
Ta có đoạn \(BD = \sqrt {ab} \) cần dựng.
* Chứng minh:
Nối DA và DC. Ta có tam giác ACD vuông tại D và \(DB \bot AC\).
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\(B{D^2} = AB.BC = a.b\)
Suy ra: \(BD = \sqrt {ab} \).
Câu 15: Giữa hai tòa nhà ( kho và phân xưởng) của một nhà máy, người ta xây dựng một băng chuyền AB để chuyển vật liệu. Khoảng cách giữa hai tòa nhà là 10m, còn hai vòng quay của băng chuyền được đặt ở độ cao 8m và 4m so với mặt đất (h.7). Tìm độ dài AB của băng chuyền.
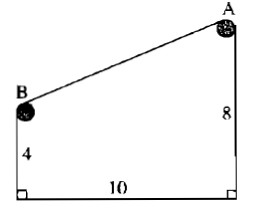

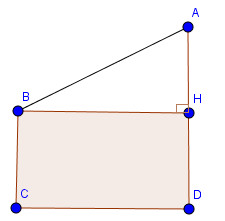
Kẻ \(BH \bot AD\) ta được tứ giác BCDH là hình chữ nhật.
Ta có: BC = DH và BH = CD (tính chất hình chữ nhật)
Suy ra: DH = 4 (m)
\(AH = 8 – 4 = 4\)(m)
BH = 10 (m)
Áp dụng định lý Pi-ta-go vào tam giác vuông ABH, ta có:
\(A{B^2} = B{H^2} + A{H^2}\)
Suy ra: \(AB = \sqrt {B{H^2} + A{H^2}} = \sqrt {{{10}^2} + {4^2}} = \sqrt {116} \approx 10,8(m)\)
Vậy băng chuyền dài khoảng 10,8m.
Câu 16: Cho tam giác có độ dài các cạnh là 5, 12, 13. Tìm góc đối diện với cạnh có độ dài 13 của tam giác.

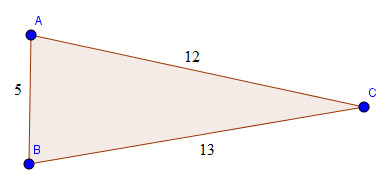
Ta có: \({5^2} + {12^2} = 25 + 144 = 169 = {13^2}\)
Vì tam giác có ba cạnh với độ dài các cạnh thỏa mãn định lý Pi-ta-go (bình phương một cạnh bằng tổng bình phương hai cạnh còn lại) nên nó là tam giác vuông.
Vậy góc đối diện với cạnh 13 ( cạnh dài nhất) là góc vuông.

