Câu 25:
a) Tìm hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm A(2;1) ;
b) Tìm hệ số của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1;-2) ;
c) Vẽ đồ thị của các hàm số với hệ số góc tìm được ở các câu a) , b) trên cùng một mặt phẳng tọa độ và chừng tỏ rằng hai đường thẳng đó vuông góc với nhau.

Đường thẳng đi qua gốc tọa độ có dạng y = ax + b.
a) Vì đường thẳng y = ax + b đi qua điểm A(2;1) nên tọa độ điểm A nghiệm đúng với phương trình đường thẳng.
Ta có : \(1 = a.2 \Leftrightarrow a = {1 \over 2}\)
Vậy hệ số góc mà đường thẳng đi qua gốc tọa độ và đi qua điểm A(2;1) là \(a = {1 \over 2}\).
b) Vì đường thẳng y = ax đi qua điểm B(1;-2) nên tọa độ điểm B nghiệm đúng phương trình đường thẳng.
Ta có: \9 – 2 = a.1 \Leftrightarrow a = – 2\)
Vậy hệ số góc của đường thẳng đi qua gốc tọa độ và đi qua điểm B(1;-2)
Là a = -2.
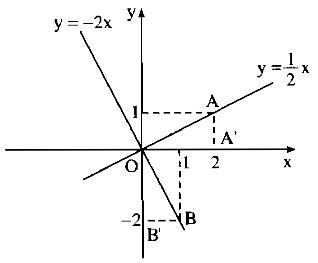
c) Với \(a = {1 \over 2}\) ta có hàm số: \(y = {1 \over 2}x\)
Với a = -2 ta có hàm số : \(y = – 2x\)
*Vẽ đồ thị hàm số \(y = {1 \over 2}x\)
Cho x = 0 thì y = 0 . Ta có: O(0;0)
Cho x = 2 thì y = 1 . Ta có: A(2;1)
Đồ thị hàm số \(y = {1 \over 2}x\) đi qua O và A.
*Vẽ đồ thị hàm số y = -2x
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = -2 . Ta có : B(1;-2)
Đồ thị hàm số y = -2x đi qua điểm O và B.
*Gọi A’, B’ lần lượt là hình chiếu của A, B trên Ox, Oy.
Ta có hai tam giác AA’O và BB’O có hai cạnh góc vuông tương ứng bằng nhau nên chúng bằng nhau.
Suy ra : \(\widehat {AOA’} = \widehat {BOB’}\) (1)
Vì \({\rm{Ox}} \bot {\rm{Oy}}\) nên \(\widehat {BOA’} + \widehat {BOB’} = {90^0}\) (2)
Từ (1) và (2) suy ra : \(\widehat {BOA’} + \widehat {AOA’} = {90^0}\)
Vậy \(OA \bot OB\) hay hai đường thẳng \(y = {1 \over 2}x\) và y = -2x vuông góc với nhau.
Câu 26: Cho hai đường thẳng
Advertisements (Quảng cáo)
y = ax + b (d)
y = a’x + b’ (d’)
Chứng minh rằng :
Trên cùng một mặt phẳng tọa độ , hai đường thẳng (d) và (d’) vuông góc với nhau khi và chỉ khi a. a’ = 1.

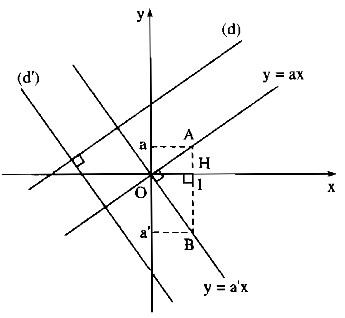
Qua gốc tọa độ , kẻ đường thẳng y = ax // (d) và y = ax // (d’).
*Chứng mình (d) vuông góc với (d’) thì a. a’ = -1
Không mất tính tổng quát, giả sử a > 0
Khi đó góc tạo bởi tia Ox và đường thẳng y = ax là góc nhọn.
Suy ra góc tạo bởi tia Ox và đường thẳng y = a’x là góc tù ( vì các góc tạo bởi
đường thẳng y = ax và đường thẳng y = a’x với tia Ox hơn kém nhau ).
Suy ra: a’ < 0
Mà đường thẳng y = ax đi qua A(1;a), đường thẳng y = a’x đi qua B(1;a’)
nên đoạn AB vuông góc với Ox tại điểm H có hoành độ bằng 1.
Vì \(\left( {\rm{d}} \right) \bot \left( {{\rm{d’}}} \right)\) nên hai đường thẳng y = ax và y = a’x vuông góc với nhau
Suy ra: \(\widehat {AOB} = {90^0}\)
Tam giác vuông AOB có \(OH \bot AB\). Theo hệ thức lượng trong tam giác vuông ta có : \(O{H^2} = HA.HB\)
Hay: \(a.\left| {a’} \right| = 1 \Leftrightarrow a.\left( { – a’} \right) = 1 \Leftrightarrow a.a’ = – 1\)
Advertisements (Quảng cáo)
Vậy nếu (d) vuông góc với (d’) thì a.a’ = -1
*Chứng minh \9a.a’ = – 1\) thì (d) vuông góc với (d’)
Ta có : \(a.a’ = – 1 \Leftrightarrow a.\left| {a’} \right| = 1\) hay \(HA.HB = O{H^2}\)
Suy ra: \({{HA} \over {OH}} = {{OH} \over {HB}} \Rightarrow \widehat {OHA} = \widehat {OHB} = {90^0}\)
Suy ra: \(\Delta OHA\) đồng dạng \(\Delta BHO \Rightarrow \widehat {AOH} = \widehat {OBH}\)
Mà \(\widehat {OBH} = \widehat {BOH} = {90^0} \Rightarrow \widehat {AOH} = \widehat {BOH} = {90^0}\)
Suy ra \(OA \bot OB\) hay hai đường thẳng y = ax và y = a’x vuông góc với nhau hay \(\left( {\rm{d}} \right) \bot \left( {{\rm{d’}}} \right)\).
Câu 27:
a) Vẽ trên cùng một mặt phẳng tọa độ đồ thị của các hàm số sau:
y = x (1)
y = 0,5x (2)
b) Đường thẳng (d) song song với trục Ox và cắt trục tung Oy tại điểm C
có tung độ bằng 2, theo thứ tự cắt các đường thẳng (1) và (2) tại D và E.
Tìm tọa độ của các điểm D, E . Tính chu vi và diện tích của tam giáo ODE.

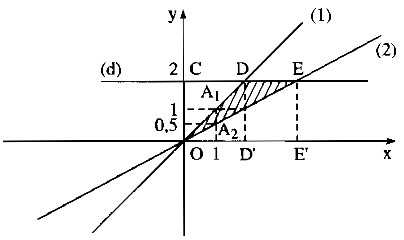
a) * Vẽ đồ thị hàm số y = x
Cho x = 0 thì y = 0. Ta có : O(0;0)
Cho x = 1 thì y = 1. Ta có: A(1;1)
Đồ thị hàm số y = x đi qua O và A.
* Vẽ đồ thị hàm số y = 0,5x
Cho x = 0 thì y = 0.Ta có : O(0;0)
Cho x = 2 thì y = 1. Ta có : B(2;1)
Đồ thị hàm số y = 0,5x đi qua O và B .
b) Qua điểm C trên trục tung có tung độ bằng 2, kẻ đường thẳng song song với Ox
cắt đồ thị hàm số y = x tại D , cắt đồ thị hàm số y = 0,5x tại E.
Điểm D có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = x ta được x = 2
Vậy điểm D(2;2)
Điểm E có tung độ bằng 2.
Thay giá trị y = 2 vào hàm số y = 0,5x ta được x = 4.
Vậy điểm E(4;2)
Gọi D’ và E’ lần lượt là hình chiều của D và E trên Ox.
Ta có: OD’ = 2, OE’ = 4.
Áp dụng định lý Pi-ta-go vào tam giác vuông ODD’, ta có:
\(O{D^2} = OD{‘^2} + {\rm{DD}}{‘^2} = {2^2} + {2^2} = 8\)
Suy ra: \(OD = \sqrt 8 = 2\sqrt 2 \)
Áp dụng định lý Pi-ta-go vào tam giác vuông OEE’, ta có:
\(O{E^2} = OE{‘^2}{\rm{ + EE}}{{\rm{‘}}^2} = {4^2} + {2^2} = 20\)
Suy ra: \(OE = \sqrt {20} = 2\sqrt 5 \)
Lại có: \(DE = CE – CD = 4 – 2 = 2\)
Chu vi tam giác ODE bằng:
\(\eqalign{
& OD + DE + EO \cr
& = 2\sqrt 2 + 2 + 2\sqrt 2 \cr
& = 2\left( {\sqrt 2 + 1 + \sqrt 5 } \right) \cr} \)
Diện tích tam giác ODE bằng: \({1 \over 2}DE.OC = {1 \over 2}.2.2 = 2\)

