Câu 36: a) Vẽ đồ thị của các hàm số sau trên cùng một mặt phẳng tọa độ
\(y = 3x + 6\); (1)
\(y = x + 2\); (2)
\(y = 2x + 4\); (3)
\(y = {1 \over 2}x + 1\). (4)
b) Gọi giao điểm của các đường thẳng (1), (2), (3), (4) với trục hoành là A và với trục tung lần lượt là \({B_1},{B_2},{B_3},{B_4}\) , ta có \(\widehat {{B_1}Ax} = {\alpha _1};\widehat {{B_2}Ax} = {\alpha _2}\); \(\widehat {{B_3}Ax} = {\alpha _3};\widehat {{B_4}Ax} = {\alpha _4}\). Tính các góc \({\alpha _1},{\alpha _2},{\alpha _3},{\alpha _4}\).
( Hướng dẫn : Dùng máy tính bỏ túi CASIO fx – 220 hoặc CASIO fx – 500A hoặc CASIO fx – 500MS … tính \(tg{\alpha _1},tg{\alpha _2},tg{\alpha _3},tg{\alpha _4}\) rồi tính ra các góc tương ứng).
c) Có nhận xét gì về độ dốc của các đường thẳng (1), (2) , (3) , (4) ?

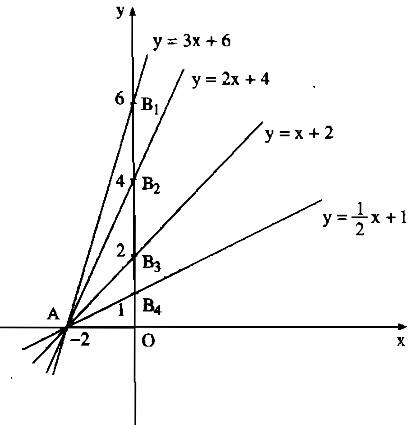
a) * Vẽ đồ thị của hàm số y = 3x + 6
Cho x = 0 thì y = 6. Ta có: \({B_1}\left( {0;6} \right)\)
Cho y = 0 thì \(3x + 6 = 0 \Leftrightarrow x = – 2\). Ta có : A(-2 ; 0)
Đồ thị của hàm số y = 3x + 6 là đường thẳng \(A{B_1}\)
* Vẽ đồ thị của hàm số y = 2x + 4
Cho x = 0 thì y = 4 . Ta có: \({B_2}\left( {0;4} \right)\)
Cho y = 0 thì \(2x + 4 = 0 \Leftrightarrow x = – 2\). Ta có : A(-2; 0)
Đồ thị của hàm số y = 2x + 4 là đường thẳng \(A{B_2}\) .
* Vẽ đồ thị của hàm số y = x + 2
Cho x = 0 thì y = 2. Ta có: \({B_3}(0;2)\)
Cho y = 0 thì \(x + 2 = 0 \Leftrightarrow x = – 2\). Ta có: \({\rm{A}}\left( { – 2;0} \right)$\)
Đồ thị của hàm số y = x + 2 là đường thẳng \(A{B_3}\)
* Vẽ đồ thị của hàm số \(y = {1 \over 2}x + 1\)
Cho x = 0 thì y = 1. Ta có: \({B_4}\left( {0;1} \right)\)
Cho y = 0 thì \({1 \over 2}x + 1 = 0 \Leftrightarrow x = – 2\). Ta có: \({\rm{A}}\left( { – 2;0} \right)\)
Đồ thị của hàm số \(y = {1 \over 2}x + 1\) là đường thẳng \(A{B_4}\)
b) Ta có:
\(tg{\alpha _1} = 3 \Rightarrow \alpha = {71^0}34’\)
\(\eqalign{
& tg{\alpha _2} = 2 \Rightarrow {\alpha _2} = {63^0}26′ \cr
& tg{\alpha _3} = 1 \Rightarrow {\alpha _3} = {45^0} \cr
& tg{\alpha _4} = {1 \over 2} \Rightarrow {\alpha _4} = {26^0}34′ \cr} \)
c) Góc tạo bởi các đường thẳng với trục Ox:
\({26^0}34′ < {45^0} < {63^0}26′ < {74^0}34’\)
Độ dốc của các đường thẳng: \(\left( 1 \right) > \left( 2 \right) > \left( 3 \right) > \left( 4 \right)\).
Câu 37: a) Cho các điểm M(-1 ; -2) , N(-2; -4), P(2; -3) , Q(3; -4,5). Tìm tọa độ của các điểm M’, N’, P’, Q’ lần lượt đồi xứng với các điểm M,N,P,Q qua trục Ox.
Advertisements (Quảng cáo)
b) Vẽ đồ thị của các hàm số sau trên cùng hệ trục tọa độ:
\(\eqalign{
& y = \left| x \right| \cr
& y = \left| {x + 1} \right| \cr} \) .
c) Tìm tọa độ giao điểm của đồ thị của các hàm số \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\).
Từ đó , suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất.

a) Hình a
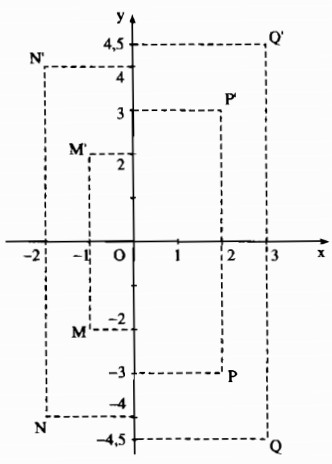
Tọa độ các điểm M’, N’, P’ , Q’ lần lượt đối xứng với các điểm M , N, P, Q qua trục Ox:
\(M’\left( {1 – ;2} \right),N’\left( { – 2;4} \right),P’\left( {2;3} \right),Q’\left( {3;4,5} \right)\)
b) Hình b
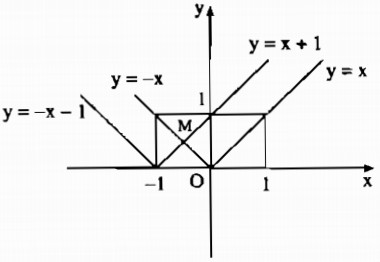
*Ta có:
\(y = \left| x \right| = \left\{ \matrix{
x\,\,\,\,\,\,\,\,\,\,\,Nếu\,\,\,x \ge 0 \hfill \cr
– x\,\,\,\,\,\,\,Nếu\,\,\,x \le 0 \hfill \cr} \right.\)
Đồ thị hàm số y = x đi qua gốc tọa độ O và điểm (1;1)
Đồ thị hàm số y = -x đi qua gốc tọa độ O và điểm (-1;1)
* Ta có :
\(y = \left| {x + 1} \right| = \left\{ \matrix{
x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,nếu\,\,\,x \ge – 1 \hfill \cr
– \left( {x + 1} \right)\,\,\,\,\,\,\,\,\,nếu\,\,\,x \le – 1 \hfill \cr} \right.\)
– Vẽ đồ thị hàm số y = x + 1
Cho x = 0 thì y = 1. Ta có: (0;1)
Cho y = 0 thì x = -1. Ta có: (-1;0)
Advertisements (Quảng cáo)
Đồ thị hàm số y = x + 1 đi qua hai điểm (0;1) và (-1;0)
– Vẽ đồ thị hàm số y = – (x + 1)
Cho x = 0 thì y = – 1. Ta có : (0;-1)
Cho y = 0 thì x = -1. Ta có : (-1;0)
Đồ thị hàm số y = – (x + 1) đi qua hai điểm (0;-1) và (-1;0)
c) Ta có : y = x và y = x + 1 song song vói nhau
y = -x và y = -(x + 1) song song vói nhau
Suy ra chỉ có đồ thị hàm số y = -x và y = x + 1 cắt nhau
Phương trình hoành độ giao điểm:
\( – x = x + 1 \Leftrightarrow 2x = – 1 \Leftrightarrow x = – {1 \over 2}\)
Suy ra phương trình \(\left| x \right| = \left| {x + 1} \right|\) có một nghiệm duy nhất.
Tung độ giao điểm: \(y = – x \Rightarrow y = {1 \over 2}\)
Vậy tọa độ giao điểm của đường thẳng \(y = \left| x \right|\) và \(y = \left| {x + 1} \right|\) là : \(I\left( { – {1 \over 2};{1 \over 2}} \right)\)
Câu 38: Cho các hàm số :
\(y = 2x – 2\); (d1)
\(y = – {4 \over 3}x – 2\); (d2)
\(y = {1 \over 3}x + 3\). (d3)
a) Vẽ đồ thị của các hàm số đã cho trên cùng một mặt phẳng tọa độ .
b) Gọi giao điểm của đường thẳng (d3) với (d1) và (d2) theo thứ tự là A, B. Tìm tọa độ của A, B
c) Tính khoảng cách AB.

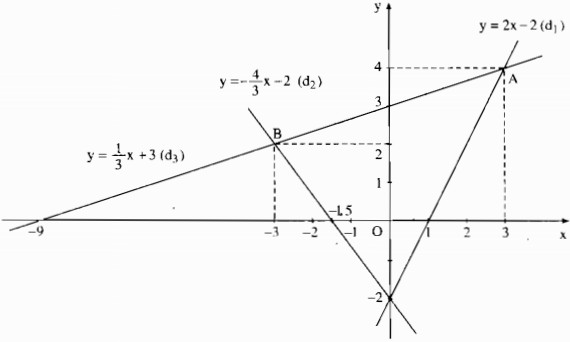
a) *Vẽ đồ thị hàm số y = 2x -2 (d1)
Cho x = 0 thì y = – 2 . Ta có :
Cho y = 0 thì 2x – 2 = 0 \( \Leftrightarrow 2x = 2 \Leftrightarrow x = 1\). Ta có: (1; 0)
Đồ thị hàm số đi qua hai điểm (0; 2) và (1; 0)
*Vẽ đồ thị hàm số \(y = – {4 \over 3}x – 2\) (d2)
Cho x = 0 thì y = -2. Ta có:
Cho y = 0 thì \( – {4 \over 3}x – 2 = 0 \Leftrightarrow x = – 1,5\) . Ta có: \(\left( { – 1,5;0} \right)\)
Đồ thị hàm số đi qua hai điểm \(\left( {0; – 2} \right)\) và \(\left( { – 1,5;0} \right)\)
* Vẽ đồ thị hàm số \(y = {1 \over 3}x + 3\) (d3)
Cho x = 0 thì y = 3. Ta có: (0;3)
Cho y = 0 thì \({1 \over 3}x + 3 = 0 \Leftrightarrow x = – 9\). Ta có: (-9; 0)
Đồ thị hàm số đi qua hai điểm (0; 3) và (-9; 0)
b) Phương trình hoành độ giao điểm của (d1) và (d3) :
\(\eqalign{
& 2x – 2 = {1 \over 3}x + 3 \cr
& \Leftrightarrow 2x – {1 \over 3}x = 3 + 2 \cr
& \Leftrightarrow {5 \over 3}x = 5 \Leftrightarrow x = 3 \cr} \)
Tung độ giao điểm: \(y = 2.3 – 2 \Leftrightarrow y = 6 – 2 = 4\)
Vậy tọa độ điểm A là : A(3; 4)
Phương trình hoành độ giao điểm của (d2) và (d3):
\(\eqalign{
& – {4 \over 3}x – 2 = {1 \over 3}x + 3 \cr
& \Leftrightarrow {1 \over 3}x + {4 \over 3}x = – 2 – 3 \cr
& \Leftrightarrow {5 \over 3}x = – 5 \Leftrightarrow x = – 3 \cr} \)
Tung độ giao điểm :
\(y = {1 \over 3}.\left( { – 3} \right) + 3 \Leftrightarrow y = – 1 + 3 = 2\)
Vậy tọa độ điểm B là : A(-3 ; 2)
c) Ta có:
\(\eqalign{
& A{B^2} = {\left( {{x_A} – {x_B}} \right)^2} + {\left( {{y_A} – {y_B}} \right)^2} \cr
& = {\left( {3 + 3} \right)^2} + {\left( {4 – 2} \right)^2} = 40 \cr
& AB = \sqrt {40} = 2\sqrt {10} \cr} \).

