Câu 4.1: Quy đồng mẫu thức ba phân thức
\({x \over {{x^2} – 2xy + {y^2} – {z^2}}}\), \({y \over {{y^2} – 2yz + {z^2} – {x^2}}}\) , \({z \over {{z^2} – 2zx + {x^2} – {y^2}}}\)

\(\eqalign{ & {x^2} – 2xy + {y^2} – {z^2} = {\left( {x – y} \right)^2} – {z^2} = \left( {x – y + z} \right)\left( {x – y – z} \right) \cr & {y^2} – 2yz + {z^2} – {x^2} = \left( {y – z + x} \right)\left( {y – z – x} \right) \cr & = – \left( {x – y + z} \right)\left( {x + y – z} \right) \cr & {z^2} – 2xz + {x^2} – {y^2} = {\left( {x – z} \right)^2} – {y^2} = \left( {x – z + y} \right)\left( {x – z – y} \right) = \left( {x + y – z} \right)\left( {x – y – z} \right) \cr} \)
MTC =\(\left( {x – y + z} \right)\left( {x + y – z} \right)\left( {x – y – z} \right)\)
\(\eqalign{ & {x \over {{x^2} – 2xy + {y^2} – {z^2}}} = {x \over {\left( {x – y + z} \right)\left( {x – y – z} \right)}} = {{x\left( {x + y – z} \right)} \over {\left( {x – y + z} \right)\left( {x + y – z} \right)\left( {x – y – z} \right)}} \cr & {y \over {{y^2} – 2yz + {z^2} – {x^2}}} = {y \over {\left( {y – z + x} \right)\left( {y – z – x} \right)}} = {{ – y} \over {\left( {x – y + z} \right)\left( {x + y – z} \right)}} \cr & = {{ – y\left( {x – y – z} \right)} \over {\left( {x – y + z} \right)\left( {x + y – z} \right)\left( {x – y – z} \right)}} \cr & {z \over {{z^2} – 2zx + {x^2} – {y^2}}} = {z \over {\left( {x + y – z} \right)\left( {x – y – z} \right)}} = {{z\left( {x – y + z} \right)} \over {\left( {x + y – z} \right)\left( {x – y + z} \right)\left( {x – y – z} \right)}} \cr} \)
Câu 4.2: Cho hai phân thức \({1 \over {{x^2} + ax – 2}}\) , \({2 \over {{x^2} + 5x + b}}\). Hãy xác định a và b biết rằng khi quy đồng mẫu thức chúng trở thành những phân thức có mẫu thức chung là\({x^3} + 4{x^2} + x – 6\). Viết tường minh hai phân thức đã cho và hai phân thức thu được sau khi quy đồng với mẫu thức chung là \({x^3} + 4{x^2} + x – 6\)
Advertisements (Quảng cáo)


Vì phép chia này là phép chia hết nên số dư phải bằng 0
Advertisements (Quảng cáo)
\( \Rightarrow a\left( {4 – a} \right) = 3\) (1) và \(2a – 8 = – 6\) (2)
Từ (2) \( \Rightarrow 2a – 8 = – 6 \Rightarrow a = 1\)
a = 1 thỏa mãn (1) ta có phân thức \({1 \over {{x^2} + x – 2}}\)
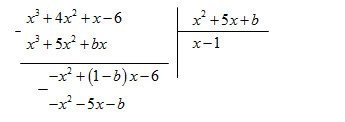
Vì phép chia này là phép chia hết nên số dư phải bằng 0
\( \Rightarrow \left( {1 – b} \right) = 5\) (3) và – b = − 6 (4)
Từ (4) ⇒ − b = − 6 ⇒ b = 6
b = 6 thỏa mãn (3) ta có phân thức \({2 \over {{x^2} + 5x + 6}}\)
\(\eqalign{ & {1 \over {{x^2} + x – 2}} = {{\left( {x + 3} \right)} \over {\left( {{x^2} + x – 2} \right)\left( {x + 3} \right)}} = {{x + 3} \over {{x^3} + 4{x^2} + x – 6}} \cr & {2 \over {{x^2} + 5x + 6}} = {{2\left( {x – 1} \right)} \over {\left( {{x^2} + 5x + 6} \right)\left( {x – 1} \right)}} = {{2x – 2} \over {{x^3} + 4{x^2} + x – 6}} \cr} \)

