Câu 19. Chứng minh rằng mỗi dãy số sau là một cấp số cộng và hãy xác định công sai của cấp số cộng đó:
a. Dãy số (un) với \(u_n= 19n – 5 \);
b. Dãy số (un) với \(u_n= an + b\), trong đó a và b là các hằng số.
a. Ta có:
\({u_{n + 1}} – {u_n} = 19\left( {n + 1} \right) – 5 – \left( {19n – 5} \right) = 19\) với mọi \(n ≥ 1\).
Do đó \((u_n)\) là một cấp số cộng với công sai \(d = 19\).
b. Ta có:
\({u_{n + 1}} – {u_n} = a\left( {n + 1} \right) + b – \left( {an + b} \right) = a\) với mọi \(n ≥ 1\).
Do đó \((u_n)\) là một cấp số cộng với công sai \(d = a\).
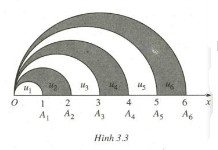
Câu 20. Trên tia Ox lấy các điểm A1, A2, …, An, … sao cho với mỗi số nguyên dương n, OAn = n. Trong cùng một nửa mặt phẳng có bờ là đường thẳng chứa tia Ox, vẽ các nửa đường tròn đường kính OAn, n = 1, 2, … . Kí hiệu u1 là diện tích của nửa hình tròn đường kính OA1 và với mỗi n ≥ 2, kí hiệu un là diện tích của hình giới hạn bởi nửa đường tròn đường kính OAn – 1 , nửa đường tròn đường kính OAn và tia Ox (h 3.3). Chứng minh rằng dãy số (un) là một cấp số cộng. Hãy xác định công sai của cấp số cộng đó.
Với \(n ≥ 2\) ta có :
\(\eqalign{
& {u_n} = {1 \over 2}\left( {\pi {{OA_n^2} \over 4} – \pi {{OA_{n – 1}^2} \over 4}} \right) \cr
& = {1 \over 8}\pi \left[ {\left( {{n^2} – {{\left( {n – 1} \right)}^2}} \right)} \right] \cr
& = {{\left( {2n – 1} \right)\pi } \over 8}\,\left( {n \ge 2} \right) \cr
& \Rightarrow {u_{n + 1}} – {u_n} = {{2n + 1} \over 8}\pi – {{\left( {2n – 1} \right)} \over 8}\pi = {\pi \over 4},\forall n \ge 2 \cr} \)
Mặt khác
\({u_2} – {u_1} = {{3\pi } \over 8} – {\pi \over 8} = {\pi \over 4}\)
Vậy \({u_{n + 1}} – {u_n} = {\pi \over 4}\;\forall n \in\mathbb N^*\)
Do đó (un) là cấp số cộng với công sai \(d = {\pi \over 4}.\)
Bài 21. Trong mỗi câu sau, hãy đánh dấu “x” vào phần kết luận mà em cho là đúng :
a. Mỗi cấp số cộng với công sai \(d > 0\) là một dãy số
 Tăng
Tăng
 Giảm
Giảm
 Không tăng cũng không giảm.
Không tăng cũng không giảm.
b. Mỗi cấp số cộng với công sai \(d < 0\) là một dãy số
 Tăng
Tăng
 Giảm
Giảm
 Không tăng cũng không giảm.
Không tăng cũng không giảm.
a. Tăng
b. Giảm
Advertisements (Quảng cáo)
Câu 22
Một cấp số cộng có năm số hạng mà tổng của số hạng đầu và số hạng thứ ba bằng 28, tổng của số hạng thứ ba và số hạng cuối bằng 40. Hãy tìm cấp số cộng đó.
Với mỗi \(n \in \left\{ {1,{\rm{ }}2,{\rm{ }}3,{\rm{ }}4,{\rm{ }}5} \right\}\), kí hiệu un là số hạng thứ n của cấp số cộng đã cho.
Ta có:
\(\eqalign{
& 28 = {u_1} + {u_3} = 2{u_2} \Rightarrow {u_2} = 14, \cr
& 40 = {u_3} + {u_5} = 2{u_4} \Rightarrow {u_4} = 20, \cr
& 2{u_3} = {u_2} + {u_4} = 34 \Rightarrow {u_3} = 17. \cr} \)
Ta có:
\(\eqalign{
& {u_1} + {u_3} = 28 \Rightarrow {u_1} = 28 – {u_3} = 11 \cr
& {u_3} + {u_5} = 40 \Rightarrow {u_5} = 40 – {u_3} = 23 \cr} \)
Vậy cấp số cộng cần tìm là : \(11, 14, 17, 20, 23\)
Câu 23. Cho cấp số cộng (un) có \(u_{20}= -52\) và \(u_{51}= -145\). Hãy tìm số hạng tổng quát của cấp số cộng đó.
Gọi \(d\) là công sai của cấp số cộng.
Ta có:
\(\left\{ {\matrix{{{u_{20}} = – 52} \cr {{u_{51}} = – 145} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{{u_1} + 19d = – 52} \cr {{u_1} + 50d = – 145} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{{u_1} = 5} \cr {d = – 3} \cr} } \right.\)
Vậy
\(\eqalign{
& {u_n} = {u_1} + \left( {n – 1} \right)d = 5 + \left( {n – 1} \right)\left( { – 3} \right) \cr
& {u_n} = – 3n + 8 \cr} \)
Câu 24. Cho cấp số cộng (un) với công sai d và cho các số nguyên dương m và k, với \(m ≥ k\). Chứng minh rằng \({u_m} = {u_k} + \left( {m-k} \right)d\).
Áp dụng : Hãy tìm công sai d của cấp số cộng (un) mà \({u_{18}} – {u_3} = 75\).
Advertisements (Quảng cáo)
Ta có:
\(\eqalign{
& {u_m} = {u_1} + \left( {m – 1} \right)d\,\left( 1 \right) \cr
& {u_k} = {u_1} + \left( {k – 1} \right)d\,\left( 2 \right) \cr} \)
Lấy (1) trừ (2) ta được :
\({u_m} – {u_k} = \left( {m – k} \right)d \Rightarrow {u_m} = {u_k} + \left( {m – k} \right)d\)
Áp dụng :
Ta có:
\(\eqalign{
& {u_{18}} – {u_3} = \left( {18 – 3} \right)d = 15d = 75 \cr
& \Rightarrow d = 5 \cr} \)
Câu 25. Cho cấp số cộng (un) có \({u_1} – {u_3} = 6\) và \(u_5= -10\). Hãy tìm công sai và số hạng tổng quát của cấp số cộng đó.
Gọi \(d\) là công sai của cấp số cộng
Ta có:
\(\left\{ {\matrix{{{u_1} – {u_3} = 6} \cr {{u_5} = – 10} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{{u_1} – \left( {{u_1} + 2d} \right) = 6} \cr {{u_1} + 4d = – 10} \cr} } \right. \Leftrightarrow \left\{ {\matrix{{d = – 3} \cr {{u_1} = 2} \cr} } \right.\)
Vậy \(d = -3\) và \({u_n} = {u_1} + \left( {n – 1} \right)d = 2 – 3\left( {n – 1} \right) = – 3n + 5\)
Câu 26. Hãy chứng minh định lí 3.
Ta sẽ chứng minh \({S_n} = {{n\left( {{u_1} + {u_n}} \right)} \over 2}\) (1)
+) Với mọi \(n \in \mathbb N^*\), bằng phương pháp qui nạp.
+) Với \(n = 1\), ta có \({S_1} = {u_1} = {{1\left( {{u_1} + {u_1}} \right)} \over 2}.\) Như vậy (1) đúng với \(n = 1\).
+) Giả sử (1) đúng khi \(n = k, k \in \mathbb N^*\), tức là:
\({S_k} = {{k\left( {{u_1} + {u_k}} \right)} \over 2}\)
+) Ta chứng minh (1) đúng với \(n=k+1\)
\(\eqalign{
& {S_{k + 1}} = {S_k} + {u_{k + 1}} \cr
& = {{k\left( {{u_1} + {u_k}} \right)} \over 2} + {u_{k + 1}} \cr
& = {{k\left( {{u_1} + {u_{k + 1}} – d} \right) + 2{u_{k + 1}}} \over 2} \cr
& = {{k{u_1} + \left( {k + 1} \right){u_{k + 1}} + {u_{k + 1}} – kd} \over 2} \cr
& = {{k{u_1} + \left( {k + 1} \right){u_{k + 1}} + {u_1}} \over 2} \cr
& = {{\left( {k + 1} \right)\left( {{u_1} + {u_{k + 1}}} \right)} \over 2} \cr} \)
Vậy (1) đúng với \(n = k + 1\)
Vậy (1) đúng với mọi \(n \in \mathbb N^*\).
Cách khác :
Ta có:
\(\eqalign{& \left\{ {\matrix{{{S_n} = {u_1} + {u_2} + … + {u_{n – 1}} + {u_n}} \cr {{S_n} = {u_n} + {u_{n – 1}} + … + {u_2} + {u_1}} \cr} } \right. \cr & \Rightarrow 2{S_n} = \left( {{u_1} + {u_n}} \right) + \left( {{u_2} + {u_{n – 1}}} \right) + … + \left( {{u_{n – 1}} + {u_2}} \right) + \left( {{u_n} + {u_1}}\right) \cr} \)
Mà \({u_2} + {u_{n – 1}} = {u_3} + {u_{n – 2}} = … = {u_n} + {u_1}\)
Do đó \(2{S_n} = n\left( {{u_1} + {u_n}} \right) \Rightarrow {S_n} = {n \over 2}\left( {{u_1} + {u_n}} \right)\)
Câu 27. Cho cấp số cộng (un) có \({u_2} + {u_{22}} = 60\). Hãy tính tổng 23 số hạng đầu tiên của cấp số cộng đó.
Gọi \(d\) là công sai của cấp số cộng đã cho, ta có :
\({u_1} = {u_2} – d\,\text{ và }\,{u_{23}} = {u_{22}} + d\)
Do đó, áp dụng định lí 3 cho \(n = 23\), ta được :
\({S_{23}} = {{23\left( {{u_1} + {u_{23}}} \right)} \over 2} = {{23\left( {{u_2} + {u_{22}}} \right)} \over 2} = {{23.60} \over 2} = 23.30 = 690\)
Câu 28. Số đo ba góc của một tam giác vuông lập thành một cấp số cộng. Hãy tìm số đo ba góc đó.
Kí hiệu A, B, C là số đo ba góc (tính theo đơn vị đo) của tam giác vuông đã cho. Không mất tổng quát, có thể giả sử \(A ≤ B ≤ C\). Khi đó, từ giả thiết tam giác vuông suy ra \(C = 90^0\) và A, B, C theo thứ tự đó là một cấp số cộng.
Ta có:
\(\left\{ {\matrix{{A + C = 2B} \cr {A + B + C = 180^\circ } \cr} } \right. \Leftrightarrow \left\{ {\matrix{{A + 90^\circ = 2B} \cr {A + B = 90^\circ } \cr} } \right. \Leftrightarrow \left\{ {\matrix{{A = 30^\circ } \cr {B = 60^\circ } \cr} } \right.\)

