Câu 9. Tìm 5 số hạng đầu của mỗi dãy số sau :
a. Dãy số (un) với \({u_n} = {{2{n^2} – 3} \over n}\)
b. Dãy số (un) với \({u_n} = {\sin ^2}{{n\pi } \over 4} + \cos {{2n\pi } \over 3}\)
c. Dãy số (un) với \({u_n} = {\left( { – 1} \right)^n}.\sqrt {{4^n}} \)
a. Ta có
\(\eqalign{
& {u_1} = {{{{2.1}^2} – 3} \over 1} = – 1 \cr
& {u_2} = {{{{2.2}^2} – 3} \over 2} = {5 \over 2} \cr
& {u_3} = {{{{2.3}^2} – 3} \over 3} = 5 \cr
& {u_4} = {{{{2.4}^2} – 3} \over 4} = {{29} \over 4} \cr
& {u_5} = {{{{2.5}^2} – 3} \over 5} = {{47} \over 5} \cr} \)
b.
\(\eqalign{
& {u_1} = {\sin ^2}{\pi \over 4} + \cos {{2\pi } \over 3} = {1 \over 2} – {1 \over 2} = 0 \cr
& {u_2} = {\sin ^2}{\pi \over 2} + \cos {{4\pi } \over 3} = 1 – {1 \over 2} = {1 \over 2} \cr
& {u_3} = {\sin ^2}{{3\pi } \over 4} + \cos 2\pi = {1 \over 2} + 1 = {3 \over 2} \cr
& {u_4} = {\sin ^2}\pi + \cos {{8\pi } \over 3} = \cos \left( {2\pi + {{2\pi } \over 3}} \right) = – {1 \over 2} \cr
& {u_5} = {\sin ^2}{{5\pi } \over 4} + \cos {{10\pi } \over 3} = {1 \over 2} – {1 \over 2} = 0 \cr} \)
c.
\(\eqalign{
& {u_1} = – 2 \cr
& {u_2} = 4 \cr
& {u_3} = – 8 \cr
& {u_4} = 16 \cr
& {u_5} = – 32 \cr} \)
Câu 10. Tìm số hạng thứ 3 và số hạng thứ 5 của mỗi dãy số sau :
a. Dãy số (un) xác định bởi :
\({u_1} = 0\,\text{ và }\,{u_n} = {2 \over {u_{n – 1}^2 + 1}}\) với mọi \(n ≥ 2\) ;
b. Dãy số (un) xác định bởi :
\({u_1} = 1,{u_2} = – 2\,\text{ và }\,u_n={u_{n – 1}} – 2{u_{n – 2}}\) với mọi \(n ≥ 3\).
a. Ta có:
\(\eqalign{
& {u_2} = {2 \over {u_1^2 + 1}} = 2 \cr
& {u_3} = {2 \over {u_2^2 + 1}} = {2 \over {{2^2} + 1}} = {2 \over 5} \cr
& {u_4} = {2 \over {u_3^2 + 1}} = {2 \over {{4 \over {25}} + 1}} = {{50} \over {29}} \cr
& {u_5} = {2 \over {u_4^2 + 1}} = {2 \over {{{\left( {{{50} \over {29}}} \right)}^2} + 1}} = {{1682} \over {3341}} \cr} \)
b. Ta có:
\(\eqalign{
& {u_3} = {u_2} – 2{u_1} = – 2 – 2.1 = – 4 \cr
& {u_4} = {u_3} – 2{u_2} = – 4 – 2\left( { – 2} \right) = 0 \cr
& {u_5} = {u_4} – 2{u_3} = 0-2.(-4)=8 \cr} \)
Câu 11. Cho hình vuông A1B1C1D1 có các cạnh bằng 6cm. Người ta dựng các hình vuông A2B2C2D2, A3B3C3D3, …, AnBnCnDn, … theo cách sau : Với mỗi n = 2, 3, 4, … lấy các điểm An, Bn , Cn, và Dn tương ứng trên các cạnh An-1Bn-1, Bn-1Cn-1, Cn-1Dn-1và Dn-1An-1 sao cho An-1An = 1cm và AnBnCnDn là một hình vuông (h.3.2). Xét dãy số (un) với un là độ dài cạnh của hình vuông AnBnCnDn.
Hãy cho dãy số (un) nói trên bởi hệ thức truy hồi.
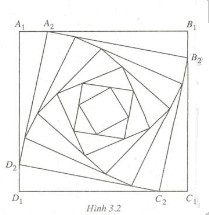
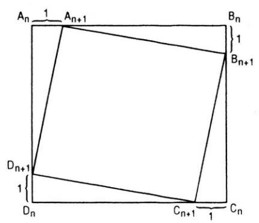
Với mỗi \(n \in \mathbb N^*\), xét các hình vuông \({A_n}{B_n}{C_n}{D_n}\) và \({A_{n + 1}}{B_{n + 1}}{C_{n + 1}}{D_{n + 1}},\) ta có
\(\eqalign{& {u_{n + 1}} = {A_{n + 1}}{B_{n + 1}} = \sqrt {{{\left( {{A_{n + 1}}{B_n}} \right)}^2} +{{\left( {{B_n}{B_{n + 1}}} \right)}^2}} \cr & = \sqrt {{{\left( {{A_n}{B_n} – 1} \right)}^2} + {1^2}} \cr & = \sqrt {{{\left( {{u_n} – 1} \right)}^2} + 1} \cr} \)
Câu 12. Cho dãy số (un) xác định bởi :
\({u_1} = 1\,\text{ và }\,{u_n} = 2{u_{n – 1}} + 3\) với mọi \(n ≥ 2\).
Bằng phương pháp quy nạp, chứng minh rằng với mọi \(n ≥ 1\) ta có \({u_n} = {2^{n + 1}}-3\) (1)
+) Với \(n = 1\) ta có \({u_1} = 1 = {2^2}-3\).
Vậy (1) đúng với \(n = 1\)
+) Giả sử (1) đúng với \(n = k\) tức là ta có : \({u_k} = {2^{k + 1}} – 3\)
+) Ta chứng minh (1) đúng với \(n = k + 1\), tức là phải chứng minh :
\({u_{k + 1}} = {2^{k + 2}} – 3\)
Thật vậy theo giả thiết qui nạp ta có :
\({u_{k + 1}} = 2{u_k} + 3 = 2\left( {{2^{k + 1}} – 3} \right) + 3 = {2^{k + 2}} – 3\)
Vậy (1) đúng với \(n = k + 1\) do đó (1) đúng với mọi \(n \in \mathbb N^*\).
Câu 13. Hãy xét tính tăng, giảm của các dãy số sau :
a. Dãy số (un) với \({u_n} = {n^3} – 3{n^2} + 5n – 7\) ;
Advertisements (Quảng cáo)
b. Dãy số (xn) với \({x_n} = {{n + 1} \over {{3^n}}}\)
c. Dãy số (an) với \({a_n} = \sqrt {n + 1} – \sqrt n \)
Hướng dẫn :
a. Xét hiệu un+1 – un.
b. Xét tỉ số \({{{x_n}} \over {{x_{n + 1}}}}\)
c. Viết lại công thức xác định an dưới dạng
\({a_n} = {1 \over {\sqrt {n + 1} + \sqrt n }}\)
Tiếp theo, xét tỉ số \({{{a_n}} \over {{a_{n + 1}}}}\)
a. Ta có:
\(\eqalign{
& {u_{n + 1}} – {u_n} = {\left( {n + 1} \right)^3} – 3{\left( {n + 1} \right)^2} + 5\left( {n + 1} \right) – 7 – \left( {{n^3} – 3{n^2} + 5n – 7} \right) \cr
& = 3{n^2} – 3n + 3 > 0,\forall n \in \mathbb N^* \cr} \)
\( \Rightarrow {u_{n + 1}} > {u_n} \Rightarrow \left( {{u_n}} \right)\) là dãy số tăng.
b. Ta có:
\(\eqalign{
& {{{x_n}} \over {{x_{n + 1}}}} = {{n + 1} \over {{3^n}}}.{{{3^{n + 1}}} \over {n + 2}} = {{3\left( {n + 1} \right)} \over {n + 2}} = {{3n + 3} \over {n + 2}} > 1\;\forall n \in \mathbb N^* \cr
& \Rightarrow {x_n} > {x_{n + 1}} \cr} \)
\(⇒ (x_n)\) là dãy số giảm.
c. Ta có:
\(\eqalign{
& {a_n} = \sqrt {n + 1} – \sqrt n = {1 \over {\sqrt {n + 1} + \sqrt n }} \cr
& {{{a_n}} \over {{a_{n + 1}}}} = {{\sqrt {n + 2} + \sqrt {n + 1} } \over {\sqrt {n + 1} + \sqrt n }} > 1 \cr
& \Rightarrow {a_n} > {a_{n + 1}} \cr} \)
⇒ \((a_n)\) là dãy số giảm.
Câu 14. Chứng minh rằng dãy số \((u_n)\) với
\({u_n} = {{2n + 3} \over {3n + 2}}\)
Là một dãy số giảm và bị chặn.
Ta có:
\(\eqalign{
& {u_n} = {{2n + 3} \over {3n + 2}} = {{{2 \over 3}\left( {3n + 2} \right) + {5 \over 3}} \over {3n + 2}} = {2 \over 3} + {5 \over {3\left( {3n + 2} \right)}} \cr
& {u_{n + 1}} – {u_n} = {5 \over 3}\left( {{1 \over {3n + 5}} – {1 \over {3n + 2}}} \right) < 0 \cr
& \Rightarrow {u_{n + 1}} < {u_n} \cr} \)
\(⇒ (u_n)\) là dãy số giảm
Ta lại có \(0 < {{2n + 3} \over {3n + 2}} \le 1 \;\forall n \in\mathbb N^*\)
Advertisements (Quảng cáo)
Vậy \((u_n)\) là dãy số giảm và bị chặn.
Câu 15. Cho dãy số (un) xác định bởi
\({u_1} = 3\,\text{ và }\,{u_{n + 1}} = {u_n} + 5\) với mọi \(n ≥ 1\).
a. Hãy tính u2, u4 và u6.
b. Chứng minh rằng \(u_n= 5n – 2\) với mọi \(n ≥ 1\).
a. Ta có:
\(\eqalign{
& {u_2} = {u_1} + 5 = 8 \cr
& {u_3} = {u_2} + 5 = 13 \cr
& {u_4} = {u_3} + 5 = 18 \cr
& {u_5} = {u_4} + 5 = 23 \cr
& {u_6} = {u_5} + 5 = 28 \cr} \)
b. Ta sẽ chứng minh : \(u_n= 5n – 2\) (1) với mọi \(n \in \mathbb N^*\), bằng phương pháp qui nạp.
+) Với \(n = 1\), ta có \(u_1= 3 = 5.1 – 2\)
Vậy (1) đúng khi \(n = 1\).
+) Giả sử (1) đúng với \(n = k, k\in \mathbb N^*\), tức là:
\(u_k=5k-2\)
+) Ta sẽ chứng minh (1) cũng đúng khi \(n = k + 1\)
Thật vậy, từ công thức xác định dãy số (un) và giả thiết qui nạp ta có :
\({u_{k + 1}} = {u_k} + 5 = 5k – 2 + 5 = 5\left( {k + 1} \right) – 2\)
Do đó (1) đúng với mọi \(n \in \mathbb N^*\).
Câu 16. Cho dãy số (un) xác định bởi
\({u_1} = 1\,\text{ và }\,{u_{n + 1}} = {u_n} + \left( {n + 1} \right){.2^n}\) với mọi \(n ≥ 1\)
a. Chứng minh rằng (un) là một dãy số tăng.
b. Chứng minh rằng
\({u_n} = 1 + \left( {n – 1} \right){.2^n}\) với mọi \(n ≥ 1\).
a. Từ hệ thức xác định dãy số (un), ta có:
\({u_{n + 1}} – {u_n} = \left( {n + 1} \right){.2^n} > 0\;\forall n \ge 1.\)
Do đó (un) là một dãy số tăng.
b. Ta sẽ chứng minh \({u_n} = 1 + \left( {n – 1} \right){.2^n}\) (1) với mọi \(n ≥ 1\), bằng phương pháp qui nạp.
+) Với \(n = 1\), ta có \({u_1} = 1 = 1 + \left( {1 – 1} \right){.2^1}.\) Như vậy (1) đúng khi \(n = 1\)
+) Giả sử (1) đúng khi \(n = k, k \in\mathbb N^*\), tức là:
\({u_k} = 1 + \left( {k – 1} \right){2^k}\)
+) Ta sẽ chứng minh (1) cũng đúng với \(n = k + 1\).
Thật vậy, từ hệ thức xác định dãy số (un) và giả thiết qui nạp, ta có :
\({u_{k + 1}} = {u_k} + \left( {k + 1} \right){.2^k} = 1 + \left( {k – 1} \right){.2^k} + \left( {k + 1} \right){.2^k} = 1 + k{.2^{k + 1}}\)
Vậy (1) đúng với mọi \(n ≥ 1\).
Câu 17. Cho dãy số (un) xác định bởi
\({u_1} = 1\,\text{ và }\,{u_{n + 1}} = {2 \over {u_n^2 + 1}}\) với mọi \(n ≥ 1\)
Chứng minh rằng (un) là một dãy số không đổi (dãy có tất cả các số hạng đều bằng nhau).
Ta chứng minh \(u_n= 1\) (1) \(∀ n \in \mathbb N^*\) bằng qui nạp
+) Rõ ràng (1) đúng với \(n = 1\)
+) Giả sử (1) đúng với \(n = k\), tức là ta có \(u_k = 1\)
+) Ta chứng minh (1) đúng với \(n = k + 1\).
Thật vậy theo công thức truy hồi và giả thiết quy nạp ta có :
\({u_{k + 1}} = {2 \over {u_k^2 + 1}} = {2 \over {1^2 + 1}}=1\)
Vậy (1) đúng với \(n = k + 1\), do đó (1) đúng với mọi \(n \in \mathbb N^*\)
Câu 18. Cho dãy số (sn) với \({s_n} = \sin \left( {4n – 1} \right){\pi \over 6}.\)
a. Chứng minh rằng \({s_n} = {s_{n + 3}}\) với mọi \(n ≥ 1\)
b. Hãy tính tổng \(15\) số hạng đầu tiên của dãy số đã cho.
a. Với \(n>1\) tùy ý, ta có :
\(\eqalign{
& {s_{n + 3}} = \sin \left[ {4\left( {n + 3} \right) – 1} \right]{\pi \over 6} \cr
& = \sin \left[ {4n – 1 + 12} \right]{\pi \over 6} \cr
& = \sin \left[ {\left( {4n – 1} \right){\pi \over 6} + 2\pi } \right] \cr
& = \sin \left( {4n – 1} \right){\pi \over 6} = {s_n} \cr} \)
b. Từ kết quả phần a ta có :
\(\eqalign{
& {s_1} = {s_4} = {s_7} = {s_{10}} = {s_{13}}, \cr
& {s_2} = {s_5} = {s_8} = {s_{11}} = {s_{14}}, \cr
& {s_3} = {s_6} = {s_9} = {s_{12}} = {s_{15}} \cr} \)
Từ đó suy ra :
\({s_1} + {s_2} + {s_3} = {s_4} + {s_5}{ + _6} = {s_7} + {s_8} + {s_9} = {s_{10}} + {s_{11}} + {s_{12}} = {s_{13}} + {s_{14}} + {s_{15}}\)
Do đó : \({S_{15}} = {s_1} + {s_2} + … + {s_{15}} = 5\left( {{s_1} + {s_2} + {s_3}} \right)\)
Bằng cách tính trực tiếp, ta có \({s_1} = 1,{s_2} = – {1 \over 2}\,\text{ và }\,{s_3} = – {1 \over 2} \Rightarrow {s_{15}} = 0\)

