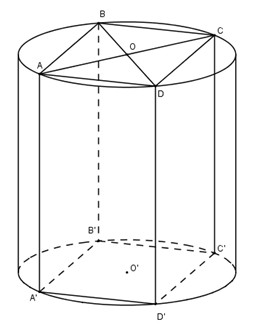
Bài 1: Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Gọi \(S\) là diện tích xung quanh của hình trụ có hai đường tròn đáy ngoại tiếp hai hình vuông \(ABCD\) và \(A’B’C’D’\). Diện tích \(S\) là:
(A) \(πa^2\); (B) \(πa^2\sqrt 2 \) ;
(C) \(πa^2\sqrt 3 \); (D) \({{\pi {{\rm{a}}^2}\sqrt 2 } \over 2}\).
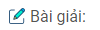
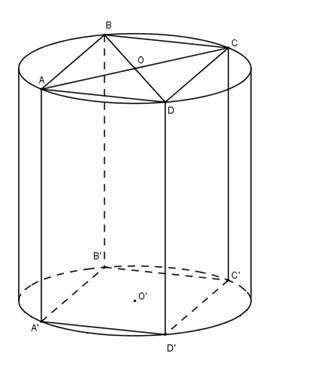
Hình trụ là hình ngoại tiếp hình vuông cạnh \(a\) nên có đường kính \( a\sqrt2\) đường cao của hình trụ là \(a\)
\(S_{xq}=\pi a\sqrt2. a=πa^2\sqrt 2 \)
Chọn (B) \(πa^2\sqrt 2 \)
Bài 2: Gọi \(S\) là diện tích xung quanh của hình nón tròn xoay được sinh ra bởi đoạn thẳng \(AC’\) của hình lập phương \(ABCD.A’B’C’D’\) có cạnh \(b\) khi quay xung quanh trục \(AA’\). Diện tích \(S\) là:
(A) \(πb^2\); (B) \(πb^2\sqrt 2 \) ;
(C) \(πb^2\sqrt 3 \) ; (D) \(πb^2\sqrt 6 \) .
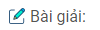
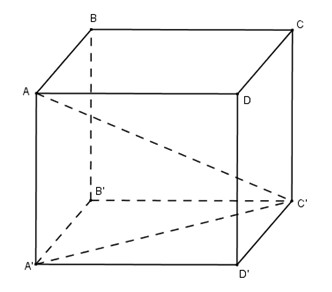
Hình nón tạo bởi khi quay \(AC’\) xung quanh \(AA’\) có đường sinh \(l=AC’=b\sqrt3\) và bán kính đáy \(C’A’=b\sqrt2\) nên \(S=\pi b\sqrt3 . b\sqrt2=πb^2\sqrt 6 \)
Chọn (D) \(πb^2\sqrt 6 \) .
Bài 3: Hình chóp \(S.ABC\) có đáy là tam giác \(ABC\) vuông tại \(A\), có \(SA\) vuông góc với mặt phẳng \((ABC)\) và có \(SA = a, AB = b, AC = c\). Mặt cầu đi qua các đỉnh \(A, B, C, S\) có bán kính \(r\) bằng:
(A) \({{2(a + b + c)} \over 3}\) ; (B) 2\(\sqrt {{a^2} + {b^2} + {c^2}} \) ;
(C) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \) ; (D) \(\sqrt {{a^2} + {b^2} + {c^2}} \) .
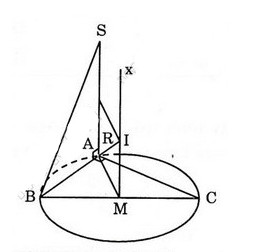
Tâm \(I\) của mặt cầu đi qua \(A,B,C,S\) là giao của trục đường tròn ngoại tiếp tam giác \(ABC\) và mặt phẳng trung trực của \(SA\)
Tam giác \(ABC\) vuông tại \(A\) nên trục đường tròn \(Mx\) với \(M\) là trung điểm của \(BC\).
Bán kính mặt cầu \(R=IA\)
\(MI={a\over 2}\), \(AM={1\over 2} BC\)
\(BC=\sqrt{b^2+c^2}\)
Do đó \(R={1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Chọn (C) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \)
Bài 4: Cho hai điểm cố định \(A, B\) và một điểm \(M\) di động trong không gian nhưng luôn thoả mãn điều kiện \(\widehat {MAB} = α\) với \(0^0<α<90^0\). Khi đó điểm \(M\) thuộc mặt nào trong các mặt sau:
(A) Mặt nón; (B) Mặt trụ;
(C) Mặt cầu; (D) Mặt phẳng.
Chọn (C) Mặt cầu.
Bài 5: Số mặt cầu chứa một đường tròn cho trước là:
(A) 0 ; (B) 1 ;
(C) 2 ; (D) vô số.
Chọn (D) vô số.
Bài 6: Trong các đa diện sau đây, đa diện nào không luôn luôn nội tiếp được trong mặt cầu:
(A) Hình chóp tam giác (tứ diện)
(B) Hình chóp ngũ giác đều;
(C) Hình chóp tứ giác;
(D) Hình hộp chữ nhật.
Chọn (C) Hình chóp tứ giác.
Advertisements (Quảng cáo)
Bài 7: Cho tứ diện \(ABCD\) có cạnh \(AD\) vuông góc với mặt phẳng \((ABC)\) và cạnh \(BD\) vuông góc với cạnh \(BC\). Khi quay các cạnh tứ diện đó xung quanh trục là cạnh \(AB\), có bao nhiêu hình nón được tạo thành?
(A) 1; (B) 2;
(C) 3; (D) 4.
Chọn (B) 2.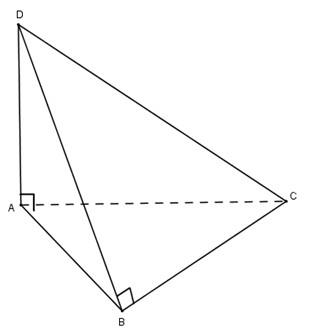
Bài 8: Cho hình lập phương \(ABCD.A’B’C’D’\) có cạnh bằng \(a\). Một hình nón có đỉnh là tâm của hình vuông \(ABCD\) và có đường tròn đáy ngoại tiếp hình vuông \(A’B’C’D’\). Diện tích xung quanh của hình nón đó là:
(A) \({{\pi {a^2}\sqrt 3 } \over 3}\) (B) \({{\pi {a^2}\sqrt 2 } \over 2}\)
(C) \({{\pi {a^2}\sqrt 3 } \over 2}\) (D) \({{\pi {a^2}\sqrt 6 } \over 2}\)
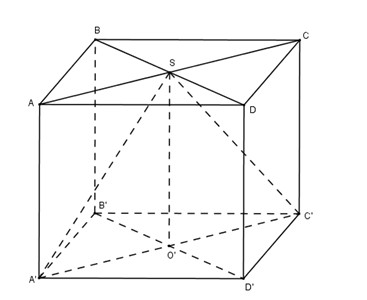
Gọi \(O\) là tâm của hình vuông \( ABCD\) thì \( OA={{a\sqrt 2 } \over 2}\)
\(\eqalign{
& OA{‘^2} = AA{‘^2} + O{A^2} \cr
& \Rightarrow OA’ = {{a\sqrt 6 } \over 2} \cr} \)
Hình nón có đường sinh \(OA’\) và và bán kính đáy là: \({{a\sqrt 2 } \over 2}\) nên có diện tích xung quanh là:
\({S_{xq}} = \pi .{{a\sqrt 2 } \over 2}.{{a\sqrt 6 } \over 2} = {{\pi {a^2}\sqrt 3 } \over 2}\)
Chọn (C) \({{\pi {a^2}\sqrt 3 } \over 2}\).
Bài 9: Cho tam giác đều \(ABC\) cạnh \(a\) quay xung quanh đường cao \(AH\) tạo nên một hình nón. Diện tích xung quanh của hình nón đó là:
(A) \(πa^2\) ; (B) \(2πa^2\) ;
(C) \({1 \over 2}πa^2\) ; (D) \({3 \over 4}πa^2\).
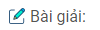
Hình nón sinh ra có bán kính đáy \(r={a\over2}\) đường sinh \(l=a\) nên có diện tích xung quanh là:
\({S_{xq}} = \pi rl = \pi {a \over 2}.a = {{\pi {a^2}} \over 2}\)
Chọn (C) \({1 \over 2}πa^2\)
Bài 10: Trong các mệnh đề sau đây, mệnh đề nào sai?
(A) Mặt trụ và mặt nón có chứa các đường thẳng.
(B) Mọi hình chóp luôn nội tiếp trong mặt cầu.
(C) Có vô số mặt phẳng cắt mặt cầu theo những đường tròn bằng nhau.
(D) Luôn có hai đường tròn có bán kính khác nhau cùng nằm trên một mặt nón.
Advertisements (Quảng cáo)
Chọn (B) Mọi hình chóp luôn nội tiếp trong mặt cầu. (Vì chỉ có hình chóp có đáy nội tiếp mới có mặt cầu ngoại tiếp).
Bài 11: Cho hình trụ có bán kính đáy bằng \(r\). Gọi \(O, O’\) là tâm của hai đáy với \(OO’ = 2r\). Một mặt cầu \((S)\) tiếp xúc với hai đáy của hình trụ tại \(O\) và \(O’\). Trong các mệnh đề dưới đây, mệnh đề nào sai?
(A) Diện tích mặt cầu bằng diện tích xung quanh của hình trụ.
(B) Diện tích mặt cầu bằng \({2 \over 3}\) diện tích toàn phần của hình trụ.
(C) Thể tích khối cầu bằng \({3 \over 4}\) thể tích khối trụ.
(D) Thể tích khối cầu bằng \({2 \over 3}\) thể tích khối trụ.
Mặt cầu có đường kính \(2r\) nên có bán kính là \(r\) và có diện tích:
\(S = 4\pi {r^2}\) và \(V = {4 \over 3}\pi {r^3}\)
Mặt trụ có bán kính \(r\) và chiều cao \(2r\) nên có:
\({S_{xq}} = 4\pi {r^2}\); \({S_{tp}} = 6\pi {r^2}\); \(V = 2\pi {r^3}\).
Chọn (C) Thể tích khối cầu bằng \({3 \over 4}\) thể tích khối trụ.
Bài 12: Một hình hộp chữ nhật nội tiếp mặt cầu và có ba kích thước là \(a, b, c\). Khi đó bán kính \(r\) của mặt cầu bằng:
(A) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \); (B) \(\sqrt {{a^2} + {b^2} + {c^2}} \);
(C) \(\sqrt {2({a^2} + {b^2} + {c^2})} \); (D) \({{\sqrt {{a^2} + {b^2} + {c^2}} } \over 3}\).
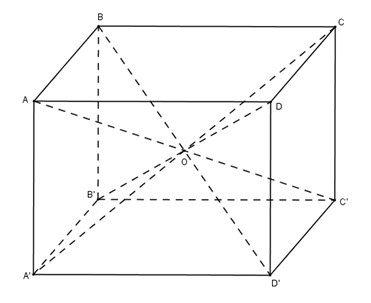
Chọn (A) \({1 \over 2}\sqrt {{a^2} + {b^2} + {c^2}} \).
Bài 13: Một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt của một hình lập phương cạnh \(a\). Thể tích của khối trụ đó là:
(A) \({1 \over 2}a^3π\) ; (B) \({1 \over 4}a^3π\) ;
(C) \({1 \over 3}a^3π\) ; (D) \(a^3π\).
Hình trụ có chiều cao bằng cạnh hình vuông \(h=a\) và bán kính đáy \(r={a\over2}\)
Chọn (B) \({1 \over 4}a^3π\).
Bài 14: Một hình tứ diện đều cạnh \(a\) có một đỉnh trùng với đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón. Khi đó diện tích xung quanh của hình nón là:
(A) \({1 \over 2}\pi {a^2}\sqrt 3 \) ; (B) \({1 \over 3}\pi {a^2}\sqrt 2 \) ;
(C) \({1 \over 3}\pi {a^2}\sqrt 3 \) ; (D) \(\pi {a^2}\sqrt 3 \) .
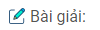
Giả sử có tứ diện đều \(ABCD\) , hình nón có đỉnh trùng với \(A\) và đáy là đường tròn ngoại tiếp tam giác \(BCD\) bán kính đường tròn đáy bằng \({2\over3}\) độ dài trung tuyến \(BCD\)
\(r = {2 \over 3}.{{a\sqrt 3 } \over 2} = {{a\sqrt 3 } \over 3}\)
Đường sinh hình nón bằng cạnh \(AB=a\).
Diện tích xung quanh của hình nón là:
\({S_{xq}} = \pi rl = {1 \over 3}\pi {a^2}\sqrt 3 \)
Chọn (C) \({1 \over 3}\pi {a^2}\sqrt 3 \).
Bài 15: Trong các mệnh đề sau đây mệnh đề nào sai?
(A) Có một mặt cầu ngoại tiếp một hình tứ diện bất kì.
(B) Có một mặt cầu ngoại tiếp một hình chóp đều.
(C) Có một mặt cầu ngoại tiếp một hình hộp.
(D) Có một mặt cầu ngoại tiếp một hình hộp chữ nhật.
Chọn (C) Có một mặt cầu ngoại tiếp một hình hộp.
Bài 16: Người ta bỏ ba quả bóng bàn cùng kích thước vào trong một chiếc hộp hình trụ có đáy bằng hình tròn lớn của quả bóng bàn và chiều cao bằng ba lần đường kính quả bóng bàn. Gọi S1 là tổng diện tích của ba quả bóng bàn, S2 là diện tích xung quanh của hình trụ. Tỉ số \({{{S_1}} \over {{S_2}}}\) bằng:
(A) 1 ; (B) 2 ;
(C) 1,5 ; (D) 1,2 .
Giải
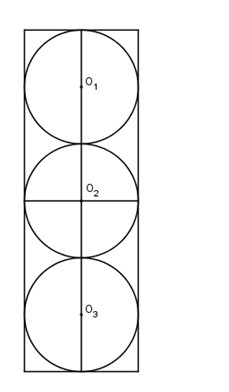
Gọi bán kính của quả cầu là \(r\) thì \(r\) cũng là bán kính đáy của hình trụ.
Chiều cao của hình trụ là \(6r\)
Chiều cao của hình trụ là \(6r\)
Diện tích xung quanh của hình trụ là: \({S_2} =2\pi r.6r= 12\pi {r^2}\)
Diện tích ba quả bóng bàn là: \({S_1} = 3.4\pi {r^2} = 12\pi {r^2}\)
Chọn (A) 1.
Bài 17: Người ta xếp \(7\) viên bi có cùng bán kính r vào một cái lọ hình trụ sao cho tất cả các viên bi đều tiếp xúc với đáy, viên bi nằm chính giữa tiếp xúc với \(6\) viên bi xung quanh và mỗi viên bi xung quanh đều tiếp xúc với các đường sinh của lọ hình trụ. Khi đó diện tích đáy của cái lọ hình trụ là:
(A) \(16πr^2\) ; (B) \(18πr^2\) ;
(C) \(9πr^2\) ; (D) \(36πr^2\) .
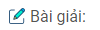
Bán kính đáy hình trụ: \(R=3r\)
Diện tích đáy hình trụ: \(S = \pi {(3r)^2} = 9\pi {r^2}\)
Chọn (C) \(9πr^2\)
Bài 18: Cho ba điểm \(A, C, B\) nằm trên một mặt cầu, biết rằng góc \(\widehat {ACB}= 90^0\). Trong các khẳng định sau, khẳng định nào là đúng?
(A) \(AB\) là một đường kính của mặt cầu.
(B) Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác \(ABC\).
(C) Tam giác \(ABC\) vuông cân tại \(C\).
(D) Mặt phẳng \((ABC)\) cắt mặt cầu theo giao tuyến là một đường tròn lớn.
Chọn (B) Luôn có một đường tròn nằm trên mặt cầu ngoại tiếp tam giác ABC.
