Giải bài 8.20 trang 57 SGK Toán 6 Kết nối tri thức với cuộc sống
Cho ba điểm A, B, C cùng nằm trên đường thẳng d sao cho B nằm giữa A và C. Hai điểm D và E không thuộc d và không cùng thẳng hàng với điểm nào trong các điểm A , B và C.
Câu a
Có bao nhiêu đường thẳng, mỗi đường thẳng đi qua ít nhất hai trong năm điểm đã cho?

– Kẻ đường thẳng DE.
– Tìm các đường thẳng đi qua D và 1 điểm trên d, các đường thẳng đi qua E và 1 điểm trên d.

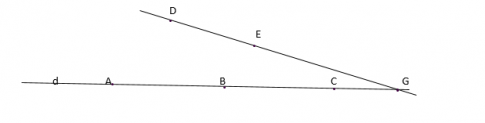
Ta cần tìm các đường thẳng đi qua 5 điểm A, B, C, D, E.
Ta đã có 2 đường thẳng là DE và d (đường thẳng đi qua A, B, C).
Đường thẳng đi qua D và 1 điểm trên d là: DA, DB, DC.
Đường thẳng đi qua E và 1 điểm trên d là: EA, EB, EC.
Vậy có 8 đường thẳng đi qua ít nhất hai trong năm điểm đã cho: DE, d, DA, DB, DC, EA, EB, EC.
Câu b
Tìm trên đường thẳng d điểm G sao cho ba điểm D, E, G thẳng hàng. Có phải khi nào cũng tìm được điểm G như thế hay không?

– Điểm G là điểm chung của hai đường thẳng.
– Hai đường thẳng không có điểm chung là hai đường thẳng song song.

Ta cần tìm điểm G nằm trên d và D, E, G thẳng hàng. Khi đó G là điểm chung của DE và d. Hay G là giao điểm của DE và d.
Không phải khi nào cũng tìm được điểm G như thế này, điểm G tồn tại khi đường thẳng DE cắt d. Khi DE và d song song với nhau thì không tồn tại điểm G.
Giải bài 8.21 trang 57 Toán 6 tập 2
Cho điểm M trên tia Om sao cho OM = 5 cm. Gọi N là điểm trên tia đối của tia Om và cách O một khoảng 7cm.
Câu a
Vẽ hình và tính độ dài đoạn thẳng MN.

– Vẽ tia Om trước.
– Lấy điểm M trên Om: Đặt thước kẻ sao cho vạch số 0 trùng với điểm O, vạch số 5 trùng với điểm M.
– Kẻ tia đối của Om: Kẻ đường có hướng ngược lại với Om.
Advertisements (Quảng cáo)
– Lấy điểm N, đo đoạn ON=7cm: tương tự khi lấy điểm M.
– Sử dụng công thức: MN=OM+ON


Vì N là điểm trên tia đối của tia Om nên ta có O nằm giữa M ,N nên ta có : ON+OM=MN
Mà OM=5cm; ON=7cm.
Vậy MN= 5+7=12 (cm).
Câu b
Gọi K là trung điểm của đoạn MN. Tính độ dài các đoạn thẳng MK và OK.

– Lấy điểm K giữa M và N sao cho đoạn thẳng NK bằng một nửa độ dài MN.
– K là trung điểm của MN nên \(MK = KN = \frac{{MN}}{2}\)
– O là điểm nằm giữa K và M nên OK + OM = KM
– Nếu OK + OM = KM thì OK = KM – OM .
– Thay độ dài các đoạn thẳng KM, OM vào công thức trên tính OK.

Vì K là trung điểm của đoạn MN nên ta có : KM=KN=MN:2=12:2=6 (cm)
Ta có : O nằm giữa M và K nên:
Advertisements (Quảng cáo)
OK + OM = KM mà KM = 6 cm; OM = 5 (cm)
Vậy OK = KM – OM = 6 – 5 = 1(cm).
Câu c
Điểm K thuộc tia nào trong hai tia OM và ON?

Quan sát hình vẽ và nhận xét vị trí của điểm.

Vì OK < MK nên K thuộc tia OM.
Bài 8.22 trang 57 SGK Toán 6 KNTT tập 2

Cho hai điểm phân biệt A và B cùng nằm trên tia Ox sao cho OA = 4 cm, OB = 6 cm. Gọi M là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng OM.

– Kẻ tia Ox, lấy OA=4cm, OB=6cm.
– Tính độ dài đoạn thẳng AB: AB=OB-OA.
– M là trung điểm của đoạn thẳng AB thì \(AM = MB = \frac{{AB}}{2}\)
– Tính độ dài đoạn thẳng OM: OM=OB-MB

Vì A và B nằm trên tia Ox nên điểm A, B nằm cùng phía đối với điểm O

Vì OA < OB nên A nằm giữa O và B nên ta có : OA+AB=OB mà OB=6 cm; OA=4 cm
Do đó AB=OB-OA=6-4=2 cm.
Vì M là trung điểm của AB nên ta có : MA=MB=AB : 2=1 cm
Vì BM < BO nên M nằm giữa O và B, ta có : OM+MB=OB mà MB=1 cm ; OB=6 cm ; OM=OB-MB=6-1=5 cm
Giải bài 8.23 Toán 6 tập 2

Trong hình vẽ dưới đây, em hãy liệt kê tất cả các bộ ba điểm thẳng hàng.


Liệt kê các bộ gồm ba điểm thẳng hàng.
3 điểm được gọi là thẳng hàng nếu 3 điểm ấy cùng nằm trên một đường thẳng.

Tất cả các điểm trên hình đều thẳng hàng với nhau nên các bộ ba các điểm thẳng hàng là các bộ 3 điểm trong 4 điểm A, B, C, N.
Các bộ ba điểm thẳng hàng là :
A,C,N và A,C,B và C,N,B và B,N,A.
Bài 8.24 trang 57 Toán 6: Luyện tập chung

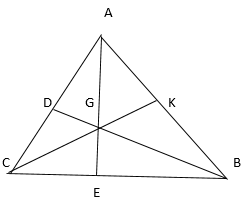
Em hãy vẽ 7 điểm trên một tờ giấy trắng sao cho có thể kẻ được 6 đường thẳng mà mỗi đường thẳng đều đi qua 3 trong 7 điểm đó.

– Lấy 3 điểm C, E, B sao cho E nằm giữa C và B.
– Lấy điểm A không thuộc đường thẳng chứa 3 điểm trên.
– Nối các đoạn AB, AC, AE.
– Lấy điểm D trên AC sao cho D nằm giữa hai điểm A và C.
– Kẻ đoạn BD.
– Lấy G là điểm chung của AE và BD.
– Nối CG.

Từ cách kẻ như trên ta được hình thỏa mãn bài toán: