Hoạt động 1 trang 34 Toán 6 Kết nối tri thức

Xét số n = \(\overline {23*} \) (* là chữ số tận cùng của n). Ta viết n = 230 + *
Số 230 có chia hết cho 2 và chia hết cho 5 không?
Thực hiện phép chia và kết luận

Số 230 chia hết cho 2 và cho 5
Hoạt động 2

Xét số n = \(\overline {23*} \) (* là chữ số tận cùng của n).
Ta viết n = 230 + *
Vận dụng tính chất chia hết của một tổng, hãy cho biết:
a) Thay dấu * bởi chữ số nào thì n chia hết cho 2?
b) Thay dấu * bởi chữ số nào thì n chia hết cho 5?
a\( \vdots \)m; b\( \vdots \)m => (a+b) \( \vdots \)m

a) Thay dấu * bởi các số 0; 2; 4; 6; 8 thì n chia hết cho 2
b) Thay dấu * bởi các số 0; 5 thì n chia hết cho 5
Luyện tập 1 trang 35 SGK Toán 6 Kết nối tri thức với cuộc sống

1. Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 2 không.
a) 1954 + 1 975; b) 2 020 – 938.
2. Không thực hiện phép tính, em hãy cho biết tổng (hiệu) sau có chia hết cho 5 không.
a) 1 945 + 2 020 ; b) 1954 – 1930.
• Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mớichia hết cho 2.
• Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
+ a\( \vdots \)m; b\( \vdots \)m => (a+b) \( \vdots \)m và a\( \vdots \)m; b\( \vdots \)m => (a – b) \( \vdots \)m

1.
a) (1 954 + 1 975 )\(\not{ \vdots }\)2
Vì 1 954 có chữ số tận cùng là 4 chia hết cho 2 và 1 975 có chữ số tận cùng là 5 không chia hết cho 2
b) (2 020 – 938) \( \vdots \) chia hết cho 2
Vì 2 020 và 938 có chữ số tận cùng là 0 và 8 nên đều chia hết cho 2.
2.
a) (1 945 + 2 020)\( \vdots \)5
Vì 1 945 và 2 020 có chữ số tận cùng là 5 và 0 nên đều chia hết cho 5
b) (1 954 – 1930) \(\not{ \vdots }\)5
Vì 1 954 có chữ số tận cùng là 4 không chia hết cho 5; 1 930 có chữ số tận cùng là 0 chia hết cho 5.
Hoạt động 3

Cho các số: 27, 82, 195, 234.
Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 9 và nhóm các số không chia hết cho 9.

Nhóm các số chia hết cho 9: 27 ; 234
Nhóm các số không chia hết cho 9: 82 ; 195
Hoạt động 4
Tính tổng các chữ số của mỗi số và xét tính chia hết cho 9 của các tổng đó trong mỗi nhóm.

Tổng các chữ số của số 9 là 9 chia hết cho 9
Tổng các chữ số của số 27 là 9 chia hết cho 9
Advertisements (Quảng cáo)
Tổng các chữ số của số 82 là 10 không chia hết cho 9
Tổng các chữ số của số 195 là 15 không chia hết cho 9
Luyện tập 2

Thay dấu * bởi một chữ số để được số \(\overline {12*} \) chia hết cho 9.
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Số \(\overline {12*} \) chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9
Hay (1 + 2 + *) chia hết cho 9
Vì 0 ≤ * ≤ 9 nên * bằng 6.
Luyện tập 3 trang 36 Toán 6 KNTT

Thay dấu * bằng một chữ số đề số \(\overline {12*5} \) chia hết cho 3.

Số \(\overline {12*5} \) chia hết cho 3 => Tổng các chữ số của nó cũng chia hết cho 3
Nên (1 + 2 + * + 5) chia hết cho 3 hay (8 + *) chia hết cho 3
Vì 0 ≤ * ≤ 9 nên * ∈ {1; 4; 7}
Trả lời Vận dụng trang 36 Toán 6 KNTT

Trên một bờ đất dài 108 m, một bác nông dân có kế hoạch trồng một số cây dừa thành một hàng sao cho hai cây cách đều nhau là 9 m và luôn có cây ở vị trí đầu và cuối của bờ đất. Hỏi bác nông dân có trồng được như vậy không? Nếu được, bác cần bao nhiêu cây dừa để trồng?


Vì 108 chia hết cho 9 nên bác nông dân có thể trồng được như thế
Số cây dừa bác cần để trồng là:
108 : 9 + 1 = 13 (cây)
Hoạt động 5

Cho các Số 42, 80, 191, 234.
Hãy sắp xếp các số trên thành hai nhóm: Nhóm các số chia hết cho 3 và nhóm các số không chia hết cho 3.

Nhóm các số chia hết cho 3: 42 ; 234
Nhóm các số không chia hết cho 3: 80 ; 191
Hoạt động 6 trang 36 Toán 6 Kết nối tri thức với cuộc sống

Advertisements (Quảng cáo)
Tính tổng các chữ số của mỗi số và xét tính chia hết cho 3 của các tổng đó trong mỗi nhóm.
– Tính tổng các chữ số của mỗi số
– Xét tính chia hết cho 3 của các tổng đó trong mỗi nhóm

Tổng các chữ số của số 42 là 6 chia hết cho 3
Tổng các chữ số của số 234 là 9 chia hết cho 3
Tổng các chữ số của số 80 là 8 không chia hết cho 3
Tổng các chữ số của số 191 là 11 không chia hết cho 3
Thử thách nhỏ trang 36 SGK Toán 6 KNTT

Bạn Hà cần tìm đường đến siêu thị. Biết rằng Hà chỉ có thể đi qua ô có chứa số chia hết cho 2 hoặc chia hết cho 3 và mỗi ô chỉ đi qua một lần. Em hãy giúp Hà đến được siêu thị nhé.
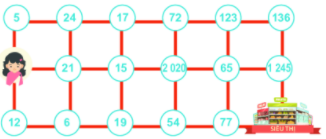

Bạn Hà có thể đi bằng 2 đường sau để đến siêu thị
12 => 6 => 21 => 15 => 2020 => 72 => 123 => 136 => 1245.
21 => 15 => 2020 => 72 => 123 => 136 => 1245.
Giải Bài 2.10 trang 37 SGK Toán 6 tập 1

Trong các số sau, số nào chia hết cho 2, số nào chia hết cho 5?
324; 248; 2020; 2025.
• Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
• Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

Các số chia hết cho 2 là: 324 ; 248 ; 2 020
Các số chia hết cho 5 là: 2 020; 2 025
Bài 2.11

Trong các số sau, số nào chia hết cho 3, số nào chia hết cho 9?
450; 123; 2 019; 2 025.
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Các số chia hết cho 3 là: 450 ; 123 ; 2 019 ; 2 025
Các số chia hết cho 9 là: 450 ; 2 025
Giải bài 2.12 trang 37 SGK Toán 6 KNTT

Khối lớp 6 của một trường có 290 học sinh đi dã ngoại. Cô phụ trách muốn chia đều số học sinh của khối 6 thành 9 nhóm. Hỏi cô có chia nhóm được như vậy không?

Tổng các chữ số của số 290 là 11 không chia hết cho 9 nên 290 không chia hết cho 9
Vậy không thể chia đều số học sinh của khối 6 thành 9 nhóm.
Bài 2.13 Toán 6 trang 37

Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Hỏi có đội nào không có đủ 9 học sinh hay không?

Tổng các chữ số của 162 là 9 chia hết cho 9 nên chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.
Bài 2.14 Toán 6 tập 1 trang 37

Thay dấu * bởi một chữ số đề số \(\overline {345*} \):
a) Chia hết cho 2 b) Chia hết cho 3;
c) Chia hết cho 5; d) Chia hết cho 9.

a) Số \(\overline {345 * } \) chia hết cho 2 thì nó phải có tận cùng là chữ số chẵn.
Vậy có thể thay * bằng các chữ số: 0; 2; 4; 6; 8
b) Số \(\overline {345 * } \) chia hết cho 3 thì tổng các chữ số của nó cũng chia hết cho 3.
Do đó 12 + * chia hết cho 3.
Mà 12 chia hết cho 3 nên * cũng chia hết cho 3
Vậy có thể thay * bằng các chữ số: 0; 3; 6; 9
c) Số \(\overline {345 * } \) chia hết cho 5 thì nó phải có tận cùng là 0 hoặc 5
Vậy có thể thay * bằng các chữ số: 0 ; 5
d) Số \(\overline {345 * } \) chia hết cho 9 thì tổng các chữ số của nó cũng chia hết cho 9
Do đó 12 + * chia hết cho 9
Vậy có thể thay * bằng chữ số 6
Giải Bài 2.15 trang 37 SGK Toán 6 KNTT tập 1

Dùng ba chữ số 3, 2, 4, hãy viết các số tự nhiên có ba chữ số khác nhau và thoả mãn một trong hai điều kiện:
a) Các số đó chia hết cho 2;
b) Các số đó chia hết cho 5.
• Các số có chữ số tận cùng là 0, 2, 4, 6, 8 thì chia hết cho 2 và chỉ những số đó mớichia hết cho 2.
• Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.

a) Các số chia hết cho 2: 304; 340 ; 430
b) Các số chia hết cho 5: 340; 430
Bài 2.16 SGK Toán 6 Kết nối tri thức với cuộc sống

Từ các chữ số 5, 0, 4, 2, viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Ta nhóm các chữ số sao cho tổng của chúng chia hết cho 3:
5 + 4 + 0 = 9; 4 + 2 + 0 = 6;
Các số cần tìm là: 504 ; 540 ; 405 ; 450 ; 420 ; 402 ; 240 ; 204.

