Câu 21: Vẽ một tam giác vuông có một góc nhọn bằng rồi viết các tỉ số lượng giác của góc .

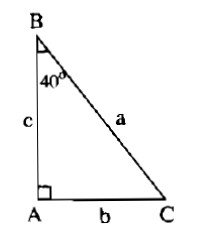
Vẽ tam giác ABC vuông tại A có \(\widehat A = {90^0},\,\widehat B = {40^0}\)
Đặt \(AB = c,AC = b,BC = a.\)
Ta có:
\(\sin 40^\circ = \sin \widehat B = {{AC} \over {BC}} = {b \over a}\)
\(\cos 40^0 = \cos \widehat B = {{AB} \over {BC}} = {c \over a}\)
\(tg{40^0} = tg\widehat B = {{AC} \over {AB}} = {b \over c}\)
\(cotg40^\circ = cotg\widehat B = {{AB} \over {AC}} = {c \over b}\)
Câu 22: Cho tam giác ABC vuông tại A. Chứng minh rằng

Advertisements (Quảng cáo)
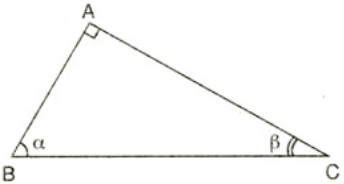
Giả sử tam giác ABC có \(\widehat A = 90^\circ \) .
Ta có: \(\sin \widehat B = {{AC} \over {BC}};\sin \widehat C = {{AB} \over {BC}}\)
Suy ra: \({{\sin \widehat B} \over {\sin \widehat C}} = {{{{AC} \over {BC}}} \over {{{AB} \over {BC}}}} = {{AC} \over {BC}}.{{BC} \over {AB}} = {{AC} \over {AB}}.\)
Câu 23: Cho tam giác ABC vuông tại A, \(\widehat B = 30^\circ ,BC = 8cm.\) Hãy tính cạnh AB (làm tròn đến chữ số thập phân thứ ba), biết rằng \(\cos 30^\circ \approx 0,866.\)

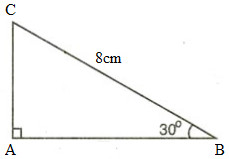
Giả sử tam giác ABC có \(\widehat A = 90^\circ ,\widehat B = 30^\circ ,BC = 8cm\).
Advertisements (Quảng cáo)
Ta có: \(\cos \widehat B = {{AB} \over {BC}}\)
Suy ra: \(AB = BC.\cos \widehat B = 8.\cos 30^\circ = 8.0,866 \approx 6,928\left( {cm} \right)\)
Câu 24: Cho tam giác ABC vuông tại A, \(AB = 6cm,\widehat B = \alpha \).
Biết \(tg\alpha = {5 \over {12}}.\) Hãy tính:
a) Cạnh AC;
b) Cạnh BC.
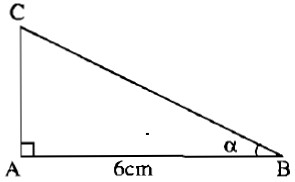

Giả sử tam giác ABC có \(\widehat A = 90^\circ ,\widehat B = \alpha .\)
a) Ta có: \(tg\alpha = tg\widehat B = {{AC} \over {AB}}\)
Suy ra: \(AC = AB.tg\widehat B = AB.tg\alpha = 6.{5 \over {12}} = 2,5\left( {cm} \right)\)
b) Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
\(B{C^2} = A{B^2} + A{C^2} = {6^2} + {(2,5)^2} = 42,25\)
Suy ra: \(BC = \sqrt {42,25} = 6,5\left( {cm} \right)\)

