Câu 5: Cho tam giác nhọn ABC. Kẻ BH vuông góc với AC (H ∈ AC) kẻ CK vuông góc với AB (K ∈ AB). Hãy so sánh \(\widehat {ABH}\) và \(\widehat {ACK}\).
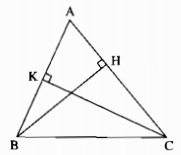
Tam giác ABH vuông tại H
\( \Rightarrow \widehat {ABH} + \widehat A = 90^\circ \) (tính chất tam giác vuông)
\( \Rightarrow \widehat {ABH} = 90^\circ – \widehat A\) (1)
Tam giác ACK vuông tại K
\( \Rightarrow \widehat {ACK} + \widehat A = 90^\circ \) (tính chất tam giác vuông)
\(\widehat {ACK} = 90^\circ – \widehat A\) (2)
Từ (1) và (2) suy ra: \(\widehat {ABH = }\widehat {ACK}\)
Câu 6: Cho tam giác ABC có \(\widehat B = \widehat C = 50^\circ \). Gọi tia Am là tia phân giác của góc ngoài ở đỉnh A. Hãy chứng tỏ Am // BC
Advertisements (Quảng cáo)
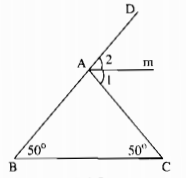
Trong ∆ABC, ta có: \(\widehat {CA{\rm{D}}}\) là góc ngoài tại đỉnh A
\(\widehat {CAD}{\rm{ = }}\widehat B + \widehat C = 50^\circ + 50^\circ = 100^\circ \) (tính chất góc ngoài của tam giác)
\(\widehat {{A_1}} = \widehat {{A_2}} = {1 \over 2}\widehat {CA{\rm{D}}} = 50^\circ \) (Vì tia Am là tia phân giác của \(\widehat {CA{\rm{D}}}\))
Suy ra: \(\widehat {{A_1}} = \widehat C = 50^\circ \)
\( \Rightarrow \) Am // BC (Vì có cặp góc ở vị trí so le trong bằng nhau)
Advertisements (Quảng cáo)
Câu 7: a) Một góc nhọn của Êke bằng 30°. Tính góc nhọn còn lại.
b) Một góc nhọn của Êke bằng 45°. Tính góc nhọn còn lại.
Vì Êke là một tam giác vuông nên:
a) Nếu một góc nhọn của Êke bằng 30° thì góc còn lại bằng:
$$90^\circ – 30^\circ = 60^\circ $$
b) Nếu một góc nhọn êke bằng 45° thì góc nhọn còn lại bằng:
$$90° – 45° = 45°$$
Câu 8: Cho tam giác ABC có \(\widehat A = 100^\circ ,\widehat B – \widehat C = 20^\circ \). Tính \(\widehat B\) và \(\widehat C\).
Trong ∆ABC, ta có:
\(\widehat A + \widehat B + \widehat C = 180^\circ \) (tổng ba góc trong tam giác)
Suy ra: \(\widehat B + \widehat C = 180^\circ – 100^\circ = 80^\circ \) (1)
\(\widehat B – \widehat C = 20^\circ \left( {gt} \right)\) (2)
Từ (1) và (2) suy ra: \(2\widehat B = 100^\circ \Rightarrow \widehat B = 50^\circ \)
Vậy \(\widehat C = 80^\circ – 50^\circ = 30^\circ \)

