Bài 1 Tổng ba góc của một tam giác SBT Toán lớp 7 tập 1. Giải bài 13, 14, 15 trang 138 Sách Bài Tập Toán lớp 7 tập 1. Câu 13: Trên hình bên có Ax song song với By…
Câu 13: Trên hình bên có Ax song song với By, \(\widehat {{\rm{CAx}}} = 50^\circ ,\widehat {CBy} = 40^\circ \). Tính \(\widehat {ACB}\) bằng cách xem nó là góc ngoài của một tam giác.
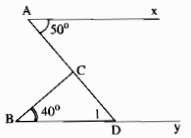
Kéo dài AC cắt By tại D.
Vì \(By{\rm{ }}//{\rm{ }}Ax{\rm{ }} = > \widehat {{D_1}} = \widehat A\) (2 góc so le trong)
Mà \(\widehat A = 50^\circ \left( {gt} \right)\) nên \(\widehat {{D_1}} = 50^\circ \)
Trong ∆DBC ta có \(\widehat {ACB}\) là góc ngoài tại đỉnh C
\( \Rightarrow \widehat {A{\rm{D}}C} = \widehat B + \widehat {{D_1}}\) (tính chất góc ngoài của tam giác)
\( \Rightarrow \widehat {A{\rm{D}}C} = 40^\circ + 50^\circ = 90^\circ \)
Câu 14: Chứng minh rằng tổng ba góc ngoài ở ba đỉnh của một tam giác thì bằng 360°.
Advertisements (Quảng cáo)
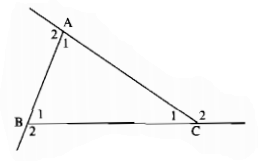
Ta có: \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ \) (hai góc kề bù)
\(\widehat {{C_1}} + \widehat {{C_2}} = 180^\circ \) (hai góc kề bù)
Suy ra: \(\widehat {{A_1}} + \widehat {{A_2}} + \widehat {{B_1}} + \widehat {{B_2}} + \widehat {{C_1}} + \widehat {{C_2}} = 180^\circ .3 = 540^\circ \)
\( \Rightarrow \widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ – \left( {\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}}} \right)\left( 1 \right)\)
Advertisements (Quảng cáo)
Trong ∆ABC ta có:
\(\widehat {{A_1}} + \widehat {{B_1}} + \widehat {{C_1}} = 180^\circ \) (tổng ba góc trong tam giác) (2)
Từ (1) và (2) suy ra:
$$\widehat {{A_2}} + \widehat {{B_2}} + \widehat {{C_2}} = 540^\circ – 180^\circ = 360^\circ $$
Câu 15: Cho tam giác ABC có \(\widehat A = 90^\circ \). Gọi E là một điểm nằm trong tam giác đó. Chứng minh rằng góc BEC là góc tù.
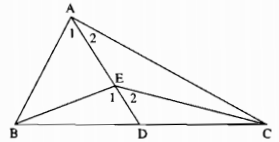
Kéo dài AE cắt BC tại D.
Trong ∆ABE ta có \(\widehat {{E_1}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_1}} > \widehat {{A_1}}\) (tính chất góc ngoài của tam giác) (1)
Trong ∆AEC ta có \(\widehat {{E_2}}\) là góc ngoài tại đỉnh E
Suy ra: \(\widehat {{E_2}} > \widehat {{A_2}}\) (tính chất góc ngoài của tam giác) (2)
Cộng từng vế (1) và (2) ra có:
\(\widehat {{E_1}} + \widehat {{E_2}} > \widehat {{A_1}} + \widehat {{A_2}}\)
Hay \(\widehat {BEC} > \widehat {BAC} = 90^\circ \)
Vậy \(\widehat {BEC}\) là góc tù

