Bài 1.29 trang 15 sách bài tập Toán 6

Áp dụng các tính chất của phép cộng để tính nhanh:
a) 21 + 369 + 79; b) 154 + 87 + 246
+ Áp dụng tính chất giao hoán, kết hợp để ghép những số hạng có tổng “đẹp” (thường là số tròn chục, tròn trăm,..) lại với nhau

a) 21 + 369 + 79 = (21 + 79) + 369 = 100 + 369 = 469
b) 154 + 87 + 246 = (154 + 246) + 87 = 400 + 87 = 487
Bài 1.30 trang 15 SBT Toán 6

Tính nhẩm bằng cách áp dụng tính chất kết hợp của phép cộng:
a) 1 597 + 65 b) 86 + 269
+ Áp dụng tính chất giao hoán, kết hợp của phép cộng
+Tách một( hay nhiều) số hạng ra thành tổng của 2(hay nhiều) số hạng. Sau đó, ghép những số hạng có tổng “đẹp” (thường là số tròn chục, tròn trăm,..) lại với nhau để dễ tính

a)1 597 + 65 = 1 597 + (3 + 62) = 1 597 + 3 + 62 = (1 597 + 3) + 62
= 1 600 + 62 = 1 662
b) *Cách 1: 86 + 269 = 86 + (14 + 255) = 86 + 14 + 255 = (86 + 14) + 255 = 100 + 255 = 355
*Cách 2: 86 + 269 = (55+31) + 269 = 55+ 31 + 269 = 55 +( 31+269) = 55+ 300= 355
Giải bài 1.31 SBT Toán 6 Kết nối tri thức

Tính nhẩm bằng cách thêm vào số hạng này và bớt ở số hạng kia cùng một số:
a) 197 + 2 135; b) 1 989 + 74
+ Thêm vào số hạng này và bớt ở số hạng kia cùng 1 số, sao cho số sau khi được thêm( hay bớt) là số “đẹp” (thường là số tròn chục, tròn trăm,..)
+ Số được thêm(bớt) nên được căn cứ vào số hạng gần tròn chục, tròn trăm,…

a) 197 + 2 135 = (197 + 3) + (2 135 – 3) = 200 + 2 132 = 2 332.
b) 1 989 + 74 = (1 989 + 11) + (74 – 11) = 2 000 + 63 = 2 063.
Bài 1.32 trang 16 sách bài tập Toán 6

Tính nhẩm bằng cách thêm (hoặc bớt) vào số bị trừ và số trừ cùng một số:
a) 876 – 197; b) 1 997 – 354
+ Cùng thêm (hoặc bớt) vào số bị trừ và số trừ cùng 1 số thì kết quả của biểu thức không đổi
+ Thêm (hoặc bớt) vào số bị trừ và số trừ cùng 1 số, sao cho số sau khi được thêm( hay bớt) là số “đẹp” (thường là số tròn chục, tròn trăm,..)
+ Số được thêm(bớt) nên được căn cứ vào số hạng gần tròn chục, tròn trăm,…

a) 876 – 197 = (876 + 3) – (197 + 3) = 879 – 200 = 679.
b) * Cách 1:
1 997 – 354 = (1997+3) – (354+3) = 2000 – 357 = 1 643
* Cách 2:
1 997 – 354 = (1 997 – 54) – (354 – 54) = 1 943 – 300 = 1 643.
Giải Bài 1.33

Tìm số tự nhiên x biết:
a) x + 257 = 981;
b) x – 546 = 35;
c) 721 – x = 615
+Tìm số hạng, ta lấy tổng trừ đi số hạng đã biết
+Số bị trừ = hiệu + số trừ
Advertisements (Quảng cáo)
+ Số trừ = số bị trừ – hiệu

a) x + 257 = 981
x = 981 – 257
x = 724
Vậy x = 724.
b) x – 546 = 35
x = 35 + 546
x = 581
Vậy x = 581.
c) 721 – x = 615
x = 721 – 615
x = 106
Vậy x = 106.
Bài 1.34 trang 16 SBT Toán lớp 6

Tính tổng:
a) 215 + 217 + 219 + 221 + 223;
b) S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20
+ Áp dụng tính chất giao hoán, kết hợp để ghép những số hạng có tổng “đẹp” (thường là số tròn chục, tròn trăm,..) lại với nhau
+ Định nghĩa phép nhân.

a) 215 + 217 + 219 + 221 + 223
= 215 + (217 + 223) + (219 + 221)
= 215 + 440 + 440
= 215 + (440 + 440)
= 215 + 880
= 1 095
a) *Cách 1:
Advertisements (Quảng cáo)
S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20
= 10 + 10 +12 +12 + 14 + 14 + 16 +16 + 18 +18 +20 + 20
= (10+20) + (12 + 18 ) + (14 +16) + (16 +14) + (18 +12) + (20 +10)
= 30 + 30 +30 + 30 +30 +30
= 30. 6
= 180
*Cách 2:
S = 2. 10 + 2. 12 + 2. 14 + … + 2. 20
= 2. 10 + 2. 12 + 2. 14 + 2. 16 + 2. 18 + 2. 20
= 20 + 24 + 28 + 32 + 36 + 40
= (20 + 40) + (24 + 36) + (28 + 32)
= 60 + 60 + 60
= 120 + 60
= 180
Giải Bài 1.35

Không thực hiện tính toán, hãy giải thích vì sao kết quả các phép tính sau đây là sai:
a) 121 + 222 + 323 + 984 + 999 = 2 648;
b) 121 + 222 + 323 + 984 + 999 = 5 649.
Sử dụng cách kiểm tra chữ số tận cùng, hay ước lượng kết quả

a) Tổng các chữ số hàng đơn vị là: 1 + 2 + 3 + 4 + 9 = (1 + 2 + 3 + 4) + 9 = 10 + 9 = 19 nên chữ số tận cùng của tổng trên phải là 9, do đó tổng bằng 2 648 là sai
b) Ta thấy: Tổng gồm 5 số hạng; các số hạng trên đều nhỏ hơn 1 000
Do đó tổng 5 số hạng trên nhỏ hơn 5 000, mà 5 649 > 5 000 nên tổng bằng 5 649 là sai
Giải bài 1.36 trang 16 sách bài tập Toán 6

Cô công nhân vệ sinh trường em nhà ở huyện Sóc Sơn (Hà Nội). Hằng ngày, cô phải đi xe đạp từ nhà ra bến xe buýt gửi xe và đi hai tuyến xe buýt, sau đó đi bộ thêm một đoạn mới đến được trường. Cô đi xe đạp khoảng 10 phút để tới được bến xe buýt; mất không quá 2 phút để gửi xe; không quá 25 phút cho tuyến xe buýt thứ nhất và không quá 15 phút cho tuyến buýt thứ hai; sau đó đi bộ từ bến xe đến trường khoảng 5 phút.
a) Trong trường hợp thuận lợi nhất (không phải chờ tuyến xe buýt nào) thì thời gian đi từ nhà đến trường của cô là bao nhiêu?
b) Để có mặt ở trường trước 5h30 (thời gian vệ sinh các lớp học là từ 5 giờ 30 phút tới 6 giờ 30 phút) cô phải ra khỏi nhà muộn nhất là mấy giờ?

a) Trong trường hợp thuận lợi nhất (không phải chờ tuyến xe buýt nào) thì tổng thời gian cô công nhân để đi từ nhà đến trường không quá:
10 + 2 + 25 + 15 + 5 = 57 (phút)
b) Muốn có mặt ở trường trước 5h30, cô phải ra khỏi nhà muộn nhất lúc:
5 giờ 30 phút – 57 phút = 4 giờ 90 phút – 57 phút = 4 giờ 33 phút.
Vậy a) Tổng thời gian cô công nhân để đi từ nhà đến trường không quá 57 phút
b) Muốn có mặt ở trường trước 5h30, cô phải ra khỏi nhà muộn nhất lúc 4 giờ 33 phút
Bài 1.37 trang 16 SBT Toán 6 KNTT

Thay các dấu ? bằng các chữ số thích hợp để được những phép tính đúng:

Tìm chữ số hàng đơn vị trước. Dựa vào tổng( hiệu) các hàng tương ứng, tìm các chữ số còn lại
a)Cần tìm các chữ số a; b; c sao cho \(\overline {8a5} + \overline {b5c} = 1504\)
b)Cần tìm các chữ số a,b,c,d sao cho \(\overline {6a2} – \overline {b8c} = \overline {d83} \)

a)Ta cần tìm các chữ số a; b; c sao cho \(\overline {8a5} + \overline {b5c} = 1504\)\((a,b,c \in N,0 \le a,b,c \le 9)\)(b>0)
Ta có: 5+ c có tận cùng là 4. Vì \(0 \le c \le 9\) nên c=9,và ta cần nhớ 1 ở hàng chục.
Khi đó, a + 5 (nhớ 1) có tận cùng là 0 nên a+5+1 có tận cùng là 0. Vì \(0 \le a \le 9\) nên \(6 \le a + 6 \le 15\)
Vậy a+6=10. Do đó, a=4, và ta cần nhớ thêm 1 ở hàng trăm
Khi đó, 8+b( nhớ 1) =15 nên b=6
Vậy phép cộng đó là 845 + 659=1504
b) Ta cần tìm các chữ số a; b; c sao cho \(\overline {6a2} – \overline {b8c} = \overline {d83} \)hay \(\overline {b8c} + \overline {d83} = \overline {6a2} \)\((a,b,c,d \in N,0 \le a,b,c,d \le 9)\)(b,d>0)
Ta có: c + 3 có tận cùng là 2, mà \(0 \le c \le 9\) nên c= 9 và ta cần nhớ 1 ở hàng chục.
Khi đó, 8+ 8( nhớ 1) có tận cùng là a. Vậy a=7, và ta cần nhớ 1 ở hàng trăm
Khi đó, b+d( nhớ 1) =6 hay b+d=5. Ta xét các trường hợp sau
Trường hợp 1: b=1 thì d = 4. Phép tính đó là 672 – 189 =483
Trường hợp 2: b=2 thì d = 3. Phép tính đó là 672 – 289 = 383
Trường hợp 3: b=3 thì d = 2. Phép tính đó là 672 – 389 = 283
Trường hợp 4: b=4 thì d = 1. Phép tính đó là 672 – 489 = 183
Bài 1.38 Sách bài tập Toán 6

Cho bảng vuông 3×3 trong đó mỗi ô được ghi một số tự nhiên sao cho tổng các số trong mỗi hàng, mỗi cột, mỗi đường chéo đều bằng nhau. Một bạn tinh nghịch xóa đi năm số ở 5 ô nên bảng chỉ còn lại như hình dưới.
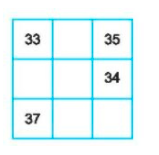
Hãy khôi phục lại bảng đã cho.
Gọi x là số ở ô chính giữa. Dựa vào các biểu thức liên hệ ( tổng các số trong mỗi hàng, mỗi cột, đường chéo là như nhau), ta tìm được các chữ số ở các ô trống

Ta cần đi tìm a,b,c,d,e
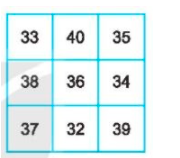
Vì tổng các số trong mỗi hàng, mỗi cột, đường chéo là như nhau nên bằng 37+ x + 35
Ta được:
*a + e + 34 = 37 + e + 35 nên a= 38
*33 + a + 37 = 35 + 34 + d, mà a= 38 nên d=39
*33 + b + 35 = 33 + a + 37, mà a= 38 nên b=40
*33+a +37 = 37 + e + 35, mà a= 38 nên e= 36
Vậy ta được bảng hoàn thiện là


