Bài 2.23 trang 36 sách bài tập Toán 6

Hãy phân tích các số A, B sau đây ra thừa số nguyên tố
A = 62.93; B = 3.82.25

\(\begin{array}{l}a)A = {6^2}{.9^3} = 6.6.9.9.9\\ = 2.3.2.3.3.3.3.3.3.3\\ = {2^2}{.3^8}\\b)B = {3.8^2}.25 = 3.2.2.2.5.5\\ = {2^3}{.3.5^2}\end{array}\)
Bài 2.24 trang 36 sách bài tập Toán 6 Kết nối tri thức với cuộc sống

Hãy phân tích các số sau ra thừa số nguyên tố:
145; 310; 2 020.

145 = 5 . 29
310 = 2 . 5 . 31
2020 = 22.5.101
Bài 2.25 trang 36 SBT Toán 6 KNTT

Tìm chữ số a để
a)\(\overline {49a} \) là số nguyên tố
b)\(\overline {23a} \) là số nguyên tố
Tra bảng số nguyên tố

Tra bảng số nguyên tố, ta được
a) a= 1 hoặc a=9
b) \(a \in \{ 0;1;2;4;5;6;7;8\} \)
Bài 2.26 trang 36 SBT Toán 6

Kiểm tra xem trong các số sau, số nào là số nguyên tố, số nào là hợp số bằng cách dùng dấu hiệu chia hết hoặc tra bảng số nguyên tố:
829; 971; 9 891; 12 344; 32 015.

Tra bảng nguyên tố ta thấy 829 và 971 là số nguyên tố
Áp dụng dấu hiệu chia hết cho 2; 3; 5 ta có:
Advertisements (Quảng cáo)
9 891 ⁝ 3( do 9 + 8 + 9 +1=27 ⁝ 3);
12 344 ⁝ 2 ( do có tận cùng là 4);
32 015 ⁝ 5 ( do có tận cùng là 5)
Vậy 9 891; 12 344; 32 015 là hợp số.
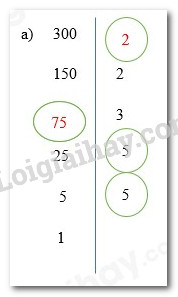
Giải Bài 2.27 sách bài tập Toán 6

Tìm các số còn thiếu trong phân tích một số ra thừa số nguyên tố theo sơ đồ cột sau đây:
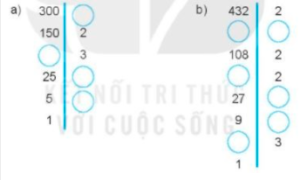

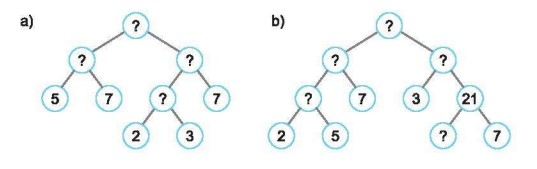
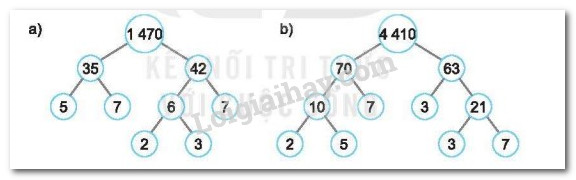
Bài 2.28 trang 36 SBT Toán 6
Tìm các số còn thiếu trong phân tích một số ra thừa số nguyên tố theo sơ đồ cây sau đây:

Bài 2.29 trang 37 SBT Toán 6

Số 2 021 có thể viết thành tổng của hai số nguyên tố được không? Vì sao?

Advertisements (Quảng cáo)
Ta thấy 2 021 là số lẻ nên phải là tổng của 1 số chẵn và 1 số lẻ
Ta có số 2 là số nguyên tố chẵn duy nhất nên ta chỉ cần xét trường hợp 2 021 = 2 + 2 019
Vì 2 019 có tổng các chữ số là 2 + 0 + 1 + 9 = 12 ⁝ 3 nên 2 019 ⁝ 3 vì thế 2 019 không phải là số nguyên tố.
Vậy 2 021 không thể viết thành tổng của hai số nguyên tố được.
Bài 2.30 trang 37 sách bài tập Toán 6

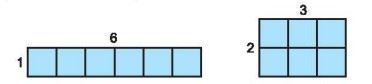
Cho 6 hình vuông đơn vị, ta có hai cách xếp chúng để tạo thành các hình chữ nhật như hình dưới đây:
a) Nếu cho 7 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
b) Nếu cho 12 hình vuông đơn vị thì ta có mấy cách xếp chúng thành các hình chữ nhật?
c) Cho n hình vuông đơn vị (n > 1). Với những số n nào thì ta chỉ có một cách xếp chúng thành hình chữ nhật? Với những số n nào thì ta có nhiều hơn một cách xếp chúng thành hình chữ nhật?

a) Ta có 7 = 7. 1
Do vậy ta có 1 cách xếp chúng thành hình chữ nhật.
Vậy ta xếp 1 hàng 7 hình vuông đơn vị
b) Ta có 12 = 12. 1 = 6. 2 = 4. 3
Do vậy ta có 3 cách xếp chúng thành hình chữ nhật.: Xếp 1 hàng 12 hình vuông đơn vị; 2 hàng mỗi hàng có 6 hình vuông đơn vị hoặc 3 hàng có 4 hình vuông đơn vị.
c) +Nếu n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật vì n = n. 1
Khi đó ta xếp 1 hàng n hình vuông đơn vị.
+ Nếu n là hợp số thì n có nhiều hơn 1 cách phân tích thành tích của các số nên có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.
Vậy khi n là số nguyên tố, ta chỉ có một cách xếp chúng thành hình chữ nhật. Khi n là hợp số thì n có nhiều hơn 1 cách sắp xếp chúng thành hình chữ nhật.
Bài 2.31 trang 37 SBT Toán 6

Tổng sau là số nguyên tố hay hợp số?
a) 11. 12. 13 + 14. 15;
b) 11. 13. 15 + 17. 19. 23

a) Vì 12 ⁝ 3 nên (11. 12. 13) ⁝ 3
15 ⁝ 3 nên (14. 15) ⁝ 3
Do đó (11. 12. 13 + 14. 15) ⁝ 3 (tính chất chia hết của một tổng)
Vậy (11. 12. 13 + 14. 15) là hợp số.
b) Ta thấy: 11. 13. 15 là tích của 3 số lẻ nên là số lẻ
17. 19. 23 là tích của 3 số lẻ nên là số lẻ
Ta được (11. 13. 15 + 17. 19. 23) là số chẵn( tổng 2 số lẻ là 1 số chẵn)
Mà (11. 13. 15 + 17. 19. 23) > 2 nên (11. 13. 15 + 17. 19. 23) là hợp số.
Vậy (11. 13. 15 + 17. 19. 23) là hợp số.
Giải Bài 2.32 trang 37 sách bài tập Toán 6 Kết nối tri thức với cuộc sống

a) Năm 1742, nhà toán học người Đức Goldbach gửi cho nhà toán học Thụy Sĩ Euler một bức thư viết rằng: Mọi số tự nhiên lớn hơn 5 đều viết được thành tổng của ba số nguyên tố, ví dụ 7 = 2 + 2 + 3; 8 = 2 + 3 + 3.
Em hãy viết các số 17; 20 thành tổng của ba số nguyên tố.
b) Trong thư trả lời Goldbach, Euler nói rằng: Mọi số chẵn lớn hơn 2 đều viết được dưới dạng tổng của hai số nguyên tố.

a) Ta có: 17 = 3 + 7 + 7;
20 = 2 + 7 + 11
b) Ta có: 36 = 17 + 19;
50 = 13 + 37.