Bài 20: Một mặt cầu gọi là nội tiếp hình nón nếu nó tiếp xúc với mặt đáy của hình nón và tiếp xúc với mọi đường sinh của hình nón. Khi đó hình nón được gọi là ngoại tiếp mặt cầu.
a) Chứng minh rằng mọi hình nón đều có một mặt cầu nội tiếp duy nhất.
b) Một hình nón có chiều cao \(h\) và bán kính đáy bằng \(r\). Hãy tính bán kính mặt cầu nội tiếp hình nón đó.
Giải
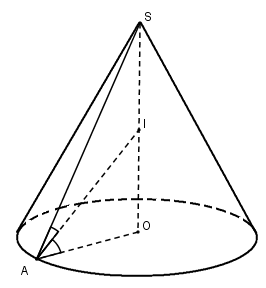
a) Cho hình nón có đỉnh \(S\) và đáy là đường tròn \((O;r)\).
Tâm \(I\) của mặt cầu nội tiếp hình nón nằm trên \(SO\). Lấy điểm \(A\) cố định trên \((O;r)\) thì \(I\) là giao điểm của \(SO\) với đường phân giác trong của góc \(A\) của \(\Delta SAO\). \(I\) hoàn toàn xác định và là tâm mặt cầu nội tiếp hình nón, bán kính mặt cầu là \(R = IO\).
b) Ta có: \(SA = \sqrt {O{S^2} + O{A^2}} = \sqrt {{h^2} + {r^2}} \)
Advertisements (Quảng cáo)
Theo tính chất đường phân giác ta có:
\({{IO} \over {IS}} = {{OA} \over {SA}} \Rightarrow {{SA} \over {SI}} = {{OA} \over {IO}} = {{SA + OA} \over {SI + IO}}\)
\(\Rightarrow {{IO} \over {IO + IS}} = {{OA} \over {OA + SA}}\)
\(\Rightarrow {{IO} \over h} = {r \over {r + \sqrt {{h^2} + {r^2}} }}\)
Advertisements (Quảng cáo)
Vậy bán kính mặt cầu nội tiếp là \(R = IO = {{rh} \over {r + \sqrt {{h^2} + {r^2}} }}\)
Bài 21: Cho tam giác \(ABC\) vuông tại \(A, AB = c, AB = b\). Tính thể tích của khối tròn xoay sinh bởi tam giác đó (kể cả các điểm trong) khi quay quanh đường thẳng \(BC\).
Giải
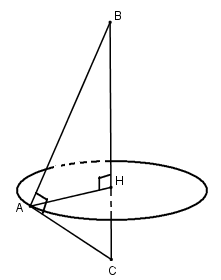
Gọi \(AH\) là đường cao của tam giác \(ABC\).
Ta có: \({1 \over {A{H^2}}} = {1 \over {A{B^2}}} + {1 \over {A{C^2}}} = {1 \over {{b^2}}} + {1 \over {{c^2}}} \Rightarrow A{H^2} = {{{b^2}{c^2}} \over {{b^2} + {c^2}}}\)
Hai tam giác \(ABH\) và \(ACH\) khi quay quanh \(BC\) lần lượt tạo thành hai khối nón \({H_1},{H_2}\) có thể tích lần lượt là
\({V_1} = {1 \over 3}\pi A{H^2}BH\,\,,\,\,{V_2} = {1 \over 3}\pi A{H^2}CH\)
Thể tích của khối tròn xoay sinh bởi tam giác \(ABC\) khi quay quanh \(BC\) là:
\(\eqalign{
& V = {V_1} + {V_2} = {1 \over 3}\pi A{H^2}BH + {1 \over 3}\pi A{H^2}CH \cr&= {1 \over 3}\pi A{H^2}BC \cr
& \,\,\,\,\, = {1 \over 3}\pi {{{b^2}{c^2}} \over {{b^2} + {c^2}}}\sqrt {{b^2} + {c^2}} = {{\pi {b^2}{c^2}} \over {3\sqrt {{b^2} + {c^2}} }} \cr} \)

