Câu 39. Tính vi phân của hàm số \(f\left( x \right) = \sin 2x\) tại điểm \(x = {\pi \over 3}\) ứng với ∆x = 0,01 ; ∆x = 0,001.
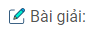
\(\eqalign{ & df\left( {{x_0}} \right) = f’\left( {{x_0}} \right)\Delta x.\,\text{ Ta có }\,f’\left( x \right) = 2\cos 2x \cr & df\left( {{\pi \over 3}} \right) = 2\cos {{2\pi } \over 3}.\Delta x = – \Delta x \cr} \)
Với \(\Delta x = 0,01\,\text{ thì }\,df\left( {{\pi \over 3}} \right) = – 0,01\)
Với \(\Delta x = 0,001\,\text{ thì }\,df\left( {{\pi \over 3}} \right) = – 0,001\)
Câu 40. Tính vi phân của các hàm số sau :
a. \(y = {{\sqrt x } \over {a + b}}\) (a và b là các hằng số)
b. \(y = xsinx\)
c. \(y = {x^2} + {\sin ^2}x\)
d. \(y = {\tan ^3}x\)
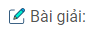
a. Ta có: \(y’ = {1 \over {2\left( {a + b} \right)\sqrt x }} \Rightarrow dy = {1 \over {2\left( {a + b} \right)\sqrt x }}dx\)
Advertisements (Quảng cáo)
b. \(y’ = \sin x + x\cos x\)
\(\Rightarrow dy = y’dx = \left( {\sin x + x\cos x} \right)dx\)
c. \(dy = y’dx = \left( {2x + \sin 2x} \right)dx\)
d. \(dy = y’dx = 3{\tan ^2}x\left( {1 + {{\tan }^2}x} \right)dx\)
Câu 41. Áp dụng công thức (2), tìm giá trị gần đúng của các số sau (làm tròn kết quả đến hàng phần nghìn).
a. \({1 \over {0,9995}}\)
b. \(\sqrt {0,996} \)
Advertisements (Quảng cáo)
c. \(\cos 45^\circ 30’\)
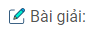
a. Xét hàm số \(f\left( x \right) = {1 \over x},\,\text{ ta có }\,f’\left( x \right) = {{ – 1} \over {{x^2}}}\)
Đặt \({x_0} = 1,\Delta x = – 0,0005\) và áp dụng công thức gần đúng
\(f\left( {{x_0} + \Delta x} \right) \approx f\left( {{x_0}} \right) + f’\left( {{x_0}} \right)\Delta x\)
Ta được : \({1 \over {{x_0} + \Delta x}} \approx {1 \over {{x_0}}} – {1 \over {x_0^2}}.\Delta x,\)
Hay : \({1 \over {0,9995}} \approx 1 + 0,0005 = 1,0005\)
b. Xét
\(\eqalign{ & f\left( x \right) = \sqrt x \,\text{ ta có }\,f’\left( x \right) = {1 \over {2\sqrt x }} \cr & {x_0} = 1,\Delta x = – 0,004 \cr & f\left( {{x_0} + \Delta x} \right) \approx f\left( {{x_0}} \right) + f’\left( {{x_0}} \right)\Delta x \cr & \Leftrightarrow \sqrt {0,996} \approx 1 – {1 \over 2}.0,004 = 0,998 \cr} \)
c. Xét hàm số \(f(x) = \cos x\), ta có: \(f’\left( x \right) = – \sin x.\)
Đặt \({x_0} = {\pi \over 4},\Delta x = {\pi \over {360}}\)
(Vì \({\pi \over {360}} = 30’\) ) và áp dụng công thức gần đúng trên, ta được :
\(\eqalign{ & \cos \left( {{\pi \over 4} + {\pi \over {360}}} \right) \approx \cos {\pi \over 4} – \sin \left( {{\pi \over 4}} \right).{\pi \over {360}} \cr & \text{Vậy }\,\cos 45^\circ 30′ \approx {{\sqrt 2 } \over 2} – {{\sqrt 2 } \over 2}.{\pi \over {360}} \approx 0,7009 \cr} \)

