Bài 9: Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) : \({(x – 5)^2} + {(y – 3)^2} = 4\). Và điểm A(1 ; 2), một đường thẳng d đi qua A và cắt đường tròn (C) theo một dây cung MN có độ dài bằng \(2\sqrt 3 \). Viết phương trình của d.

(Xem hình 3.32)
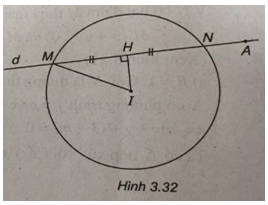
Đường tròn (C) có tâm I(5 ; 3) và có bán kính R = 2.
Gọi H là trung điểm của MN. Ta có
\(IH \bot MN\) và \(MH = {{MN} \over 2} = \sqrt 3 \)
\(IH = \sqrt {I{M^2} – M{H^2}} = \sqrt {4 – 3} = 1.\)
Phương trình đường thẳng d có dạng :
\(y – 2 = k(x – 1) \Leftrightarrow kx – y + 2 – k = 0.\)
Ta có IH = 1
\( \Leftrightarrow {{\left| {5k – 3 + 2 – k} \right|} \over {\sqrt {{k^2} + 1} }} = 1\)
\(\eqalign{
& \Leftrightarrow \left| {4k – 1} \right| = \sqrt {{k^2} + 1} \cr
& \Leftrightarrow {\left( {4k – 1} \right)^2} = {k^2} + 1 \cr} \)
\(\eqalign{
& \Leftrightarrow 15{k^2} – 8k = 0 \cr
& \Leftrightarrow \left[ \matrix{
k = 0 \hfill \cr
k = {8 \over {15}} \hfill \cr} \right. \cr} \)
Vậy có hai điểm d thỏa mãn đề bài.
Đó là \({d_1}:y – 2 = 0\)
\(\eqalign{
& {d_2}:y – 2 = {8 \over {15}}\left( {x – 1} \right) \cr
& \Leftrightarrow 8x – 15y + 22 = 0. \cr} \)
Bài 10: Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\). Gọi hai tiêu điểm của (E) lần lượt là \({F_1},{F_2}\) và M thuộc (E) sao cho \(\widehat {{F_1}M{F_2}} = {60^ \circ }\) . Tìm tọa độ điểm M và tính diện tích tam giác \(M{F_1}{F_2}\)

(Xem hình 3.33)
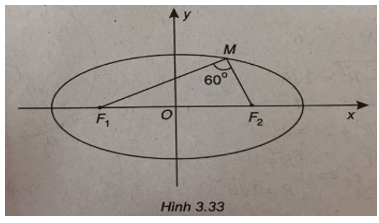
Elip (E) có phương trình chính tắc: \({{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1.\)
Ta có : a = 5, b = 3. Suy ra \({c^2} = {a^2} – {b^2} = 25 – 9 = 16.\)
Advertisements (Quảng cáo)
Vậy c = 4.
Xét điểm M(x;y) thuộc elip, ta có:
\(\left\{ \matrix{
{F_1}M = a + {c \over a}x = 5 + {4 \over 5}x \hfill \cr
{F_2}M = a – {c \over a}x = 5 – {4 \over 5}x \hfill \cr} \right.\)
Áp dụng định lí côsin trong tam giác \({F_1}M{F_2}\) ta có:
\({F_1}F_2^2 = MF_1^2 + MF_2^2 – 2M{F_1}.M{F_2}\cos {60^ \circ }\)
\( \Leftrightarrow 4{c^2} = {\left( {5 + {4 \over 5}x} \right)^2} + {\left( {5 – {4 \over 5}x} \right)^2} – 2\left( {25 – {{16} \over {25}}{x^2}} \right).{1 \over 2}\)
\(\Leftrightarrow 64 = 25 + {{48} \over {25}}{x^2} \Leftrightarrow {x^2} = {{25} \over {16}}.13 \Leftrightarrow x = \pm {5 \over 4}\sqrt {13} \,\,(1)\)
Ta lại có: \(M \in \left( E \right) \Rightarrow {{{x^2}} \over {25}} + {{{y^2}} \over 9} = 1\,\,\,\,\,(2)\)
Thay (1) vào phương trình (2) ta được:
\({{{y^2}} \over 9} = 1 – {{13} \over {16}} \Leftrightarrow {y^2} = {9 \over {16}}.3 \Leftrightarrow y = \pm {3 \over 4}\sqrt 3 .\)
Vậy có bốn điểm M thỏa mãn đề bài. Chúng có tọa độ là \(\left( { \pm {5 \over 4}\sqrt {13} ; \pm {3 \over 4}\sqrt 3 } \right).\)
Bài 11: Trong mặt phẳng tọa độ Oxy, cho ba điểm I(2 ; 4), B(1 ; 1), C(5 ; 5). Tìm điểm A sao cho I là tâm đường tròn nội tiếp tam giác ABC.

(Xem hình 3.34)
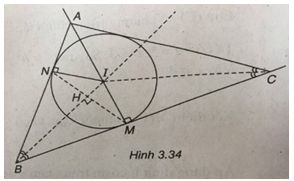
Advertisements (Quảng cáo)
Ta có : \(IB = \sqrt {{{\left( {1 – 2} \right)}^2} + {{\left( {1 – 4} \right)}^2}} = \sqrt {10} \)
\(\eqalign{
& IC = \sqrt {{{(5 – 2)}^2} + {{(5 – 4)}^2}} = \sqrt {10} \cr
& IB = IC \Rightarrow AB = AC. \cr} \)
Gọi M là trung điểm của BC, ta có M(3 ; 3).
Phương trình đường thẳng \(IM:x + y – 6 = 0\,\,\,\,\,\,\,\,\,\,(1)\)
Phương trình đường thẳng \(IB:3x – y – 2 = 0\,\,\,\,\,\,\,\,\,(2)\)
Gọi N là điểm đối xứng với M qua đường thẳng IB. Đặt N(x;y), ta có tọa độ trung điểm H của MN là \(\left( {{{x + 3} \over 2};{{y + 3} \over 2}} \right).\)
\(\overrightarrow {MN} = (x – 3;y – 3)\)
\(\overrightarrow {BI} = (1;3)\)
Ta có: \(\left\{ \matrix{
\overrightarrow {MN} .\overrightarrow {BI} = 0 \hfill \cr
H \in IB \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x – 3 + 3(y – 3) = 0 \hfill \cr
3\left( {{{x + 3} \over 2}} \right) – \left( {{{y + 3} \over 2}} \right) – 2 = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{
x + 3y – 12 = 0 \hfill \cr
3x – y + 2 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {3 \over 5} \hfill \cr
y = {{19} \over 5}. \hfill \cr} \right.\)
Vậy \(N\left( {{3 \over 5};{{19} \over 5}} \right).\)
Ta có B(1 ; 1). Phương trình đường thẳng BN: 7x + y – 8 = 0.
Điểm A là giao của hai đường thẳng BN và IM nên tọa độ của A là nghiệm của hệ phương trình
\( \Leftrightarrow \left\{ \matrix{
7x + y – 8 = 0 \hfill \cr
x + y – 6 = 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = {1 \over 3} \hfill \cr
y = {{17} \over 3} \hfill \cr} \right.\)
Vậy tọa độ điểm A là \(\left( {{1 \over 3};{{17} \over 3}} \right).\)
Bài 12: Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over {{a^2}}} + {{{y^2}} \over {{b^2}}} = 1\left( {a > b > 1} \right).\) Một góc vuông uOv (vuông tại O) quay quanh gốc O, cắt elip (E) tại M và N. Chứng minh rằng \({1 \over {O{M^2}}} + {1 \over {O{N^2}}}\) không đổi, từ đó suy ra MN luôn tiếp xúc với một đường tròn cố định.

(Xem hình 3.35)
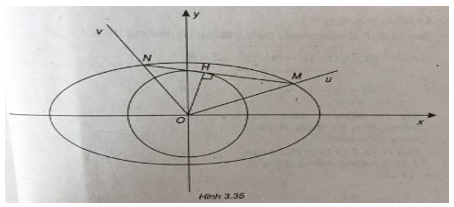
Gọi y = kx và \(y = – {1 \over k}x\) là phương trình của Ou và Ov.
Phương trình hoành độ giao điểm của Ou và elip (E):
\({{{x^2}} \over {{a^2}}} + {{{k^2}{x^2}} \over {{b^2}}} = 1 \Leftrightarrow x_M^2 = {{{a^2}{b^2}} \over {{b^2} + {k^2}{a^2}}}.\)
Ta có :
\(\eqalign{
& O{M^2} = x_M^2 + y_M^2 \cr
& = x_M^2 + {k^2}x_M^2 = x_M^2({k^2} + 1) \cr
& = {{{a^2}{b^2}(1 + {k^2})} \over {{b^2} + {k^2}{a^2}}} \cr} \)
……..
Suy ra : \({1 \over {O{M^2}}} = {{{b^2} + {k^2}{a^2}} \over {{a^2}{b^2}(1 + {k^2})}}.\)
Tương tự:
\(\eqalign{
& {1 \over {O{N^2}}} = {{{b^2} + {1 \over {{k^2}}}{a^2}} \over {{a^2}{b^2}\left( {1 + {1 \over {{k^2}}}} \right)}} \cr
& = {{{a^2} + {k^2}{b^2}} \over {{a^2}{b^2}(1 + {k^2})}}. \cr} \)
Suy ra:
\(\eqalign{
& {1 \over {O{M^2}}} + {1 \over {O{N^2}}} \cr
& = {{{a^2} + {b^2} + {k^2}\left( {{a^2} + {b^2}} \right)} \over {{a^2}{b^2}\left( {1 + {k^2}} \right)}} \cr
& = {{{a^2} + {b^2}} \over {{a^2}{b^2}}}. \cr} \)
Vậy \({1 \over {O{M^2}}} + {1 \over {O{N^2}}}\) không đổi.
Vẽ đường cao OH của tam giác vuông OMN.
Ta có : \({1 \over {O{H^2}}} = {1 \over {O{M^2}}} + {1 \over {O{N^2}}} = {{{a^2} + {b^2}} \over {{a^2}{b^2}}}.\)
Suy ra: \(OH = {{ab} \over {\sqrt {{a^2} + {b^2}} }} = R\) không đổi
Vậy MN luôn tiếp xúc với đường tròn cố định tâ O bán kính \(R = {{ab} \over {\sqrt {{a^2} + {b^2}} }}.\)

