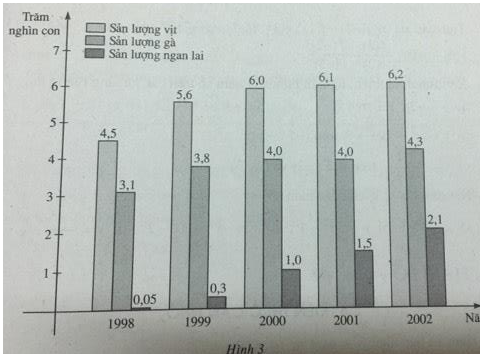
Bài 1: Biểu đồ sau (h.3) biểu thị sản lượng vịt, gà và ngan lai qua 5 năm của một
a) Tìm tập xác định của mỗi hàm số đã nêu.
b) Tìm các giá trị f(2002), g(1999), h(2000) và nêu ý nghĩa của chúng;
c) Tìm hiệu h(2002) – h(1999) và nêu ý nghĩa của nó.

a) Tập xác định của cả ba hàm số \(y = f(x),y = g(x)\) và \(y = h(x)\) là:
\(D = {\rm{\{ }}1998;1999;2000;2001;2002\} \)
b) \(f(2002) = 620000\) (con) \(g(1999) = 380000\) (con) \(h(2000) = 100000\) (con)
Năm 2002 sản lượng của trang trại là 620 000 con vịt ; năm 1999 sản lượng là 380 000 con gà ; năm 2000 trang trại có sản lượng là 100 000 con ngan lai.
c) \(h(2002) – h(1999) = 210000 – 30000 = 180000\) (con)
Sản lượng ngan lai của trang trại năm 2002 tăng 180 000 con so với năm 1999.
Advertisements (Quảng cáo)
Bài 2: Tìm tập xác định của các hàm số
a) \(y = – {x^5} + 7x – 2\)
b) \(y = {{3x + 2} \over {x – 4}}\)
c) \(y = \sqrt {4x + 1} – \sqrt { – 2x + 1} \)
d) \(y = {{\sqrt {x + 9} } \over {{x^2} + 8x – 20}}\)
e) \(y = {{2x + 1} \over {(2x + 1)(x – 3)}}\)
h) \(y = {{7 + x} \over {{x^2} + 2x – 5}}\)
Advertisements (Quảng cáo)

a) D = R;
b) D = R\{4};
c) Hàm số xác định với các giá trị của x thỏa mãn
\(4x + 1 \ge 0\) và \( – 2x + 1 \ge 0\) hay \(x \ge – {1 \over 4}\) \(x \le – {1 \over 2}\)
Vậy tập xác định của hàm số đã cho là \(D = {\rm{[}} – {1 \over 4};{1 \over 2}{\rm{]}}\)
d) Hàm số xác định với các giá trị của x thỏa mãn
\(\left\{ \matrix{
x + 9 \ge 0 \hfill \cr
{x^2} + 8x – 20 \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge – 9 \hfill \cr
x \ne – 10,x \ne 2 \hfill \cr} \right.\)
Vậy tập xác định của hàm số đã cho là \(D = {\rm{[ – 9; + }}\infty )\backslash {\rm{\{ }}2\} \)
e) \(D = R\backslash {\rm{\{ – }}{1 \over 2};3\} \)
h) \(D = R\backslash {\rm{\{ }} – 1 – \sqrt 6 ; – 1 + \sqrt 6 \} \) vì
\({x^2} + 2x – 5 = 0 \Leftrightarrow \left[ \matrix{
x = – 1 – \sqrt 6 \hfill \cr
x = – 1 + \sqrt 6 \hfill \cr} \right.\)
Bài 3: Cho hàm số
\(y = f(x) = \left\{ \matrix{
{{2x – 3} \over {x – 1}};x \le 0 \hfill \cr
– {x^2} + 2x;x > 0 \hfill \cr} \right.\)
Tính giá trị của hàm số đó tại \(x = 5;x = – 2;x = 0;x = 2\)

\(f(5) = – {5^2} + 2.5 = – 25 + 10 = – 15\) (vì 5 > 0);
\(f( – 2) = {{2.( – 2) – 3} \over { – 2 – 1}} = {7 \over 3}\) (vì -2<0); \(f(0) = 3;f(2) = 0\).

