Đề toán tổng hợp cuối năm Sách bài tập Toán Hình học 10. Giải bài 1, 2, 3, 4 trang 196, 197 Sách bài tập Toán Hình học 10. Câu 1: Trong mặt phẳng Oxy cho tam giác ABC…
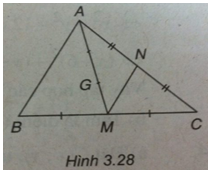
Bài 1: Trong mặt phẳng Oxy cho tam giác ABC, biết đỉnh A(1 ; 1) và tọa độ trọng tâm G(1 ; 2). Cạnh AC và đường trung trực của nó lần lượt có phương trình là x + y – 2 = 0 và – x + y – 2 = 0. Các điểm M và N lần lượt là trung điểm của BC và AC.
a) Hãy tìm tọa độ các điểm M và N.
b) Viết phương trình hai đường thẳng chứa hai cạnh AB và BC.

(h.3.28)
a) \(\eqalign{
& \overrightarrow {AM} = {3 \over 2}\overrightarrow {AG} \cr
& \Leftrightarrow \left\{ \matrix{
{x_M} – 1 = {3 \over 2}(1 – 1) \hfill \cr
{y_M} – 1 = {3 \over 2}(2 – 1) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_M} = 1 \hfill \cr
{y_M} = {5 \over 2}. \hfill \cr} \right. \cr} \)
Vậy M có tọa độ là \(\left( {1;{5 \over 2}} \right)\)
Điểm N(x ; y) thỏa mãn hệ phương trình
\(\left\{ \matrix{
x + y = 2 \hfill \cr
– x + y = 2 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x = 0 \hfill \cr
y = 2. \hfill \cr} \right.\)
b) \(\eqalign{
& \overrightarrow {AB} = 2\overrightarrow {NM} \cr
& \Leftrightarrow \left\{ \matrix{
{x_B} – 1 = 2(1 – 0) \hfill \cr
{y_B} – 1 = 2\left( {{5 \over 2} – 2} \right) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_B} = 3 \hfill \cr
{y_B} = 2. \hfill \cr} \right. \cr} \)
Đường thẳng chứa cạnh AB đi qua hai điểm A(1 ;1) và B(3 ; 2) nên có phương trình : x – 2y + 1=0.
Đường thẳng chứa cạnh BC đi qua hai điểm B(3 ; 2) và $M\left( {1;{5 \over 2}} \right)$ nên có phương trình:
x + 4y – 11 = 0
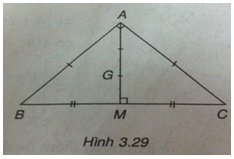
Bài 2: Trong mặt phẳng Oxy cho tam giác ABC có \(AB = AC,\,\widehat {BAC} = {90^ \circ }\). Biết M(1 ; -1) là trung điểm cạnh BC và \(G\left( {{2 \over 3};0} \right)\) là trọng tâm tam giác ABC.
Tìm tọa độ các đỉnh A, B, C.

Advertisements (Quảng cáo)
(h.3.29)
\(\eqalign{
& \overrightarrow {MA} = 3\overrightarrow {MG} \Leftrightarrow \left\{ \matrix{
{x_A} – 1 = 3\left( {{2 \over 3} – 1} \right) \hfill \cr
{y_A} + 1 = 3(0 + 1) \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{x_A} = 0 \hfill \cr
{y_A} = 2. \hfill \cr} \right. \cr} \)
Vậy A có tọa độ (0 ; 2).
Đặt B(x ; y) ta có :
\(\eqalign{
& \,\,\,\,\,\,\,\left\{ \matrix{
\overrightarrow {MB} \bot \overrightarrow {MA} \hfill \cr
M{B^2} = M{A^2} \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
\left( {x – 1} \right)\left( {0 – 1} \right) + \left( {y + 1} \right)\left( {2 + 1} \right) = 0 \hfill \cr
{\left( {x – 1} \right)^2} + {\left( {y + 1} \right)^2} = 1 + 9 \hfill \cr} \right. \cr} \)
\(\Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
{(3y + 3)^2} + {(y + 1)^2} = 10 \hfill \cr} \right.\)
\(\eqalign{
& \Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
{(3y + 3)^2} + {(y + 1)^2} = 10 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
x = 3y + 4 \hfill \cr
10{y^2} + 20y = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{
y = 0,x = 4 \hfill \cr
y = – 2,x = – 2 \hfill \cr} \right. \cr} \)
Vậy ta có tọa độ của điểm B và C như sau : B(4 ; 0), C(-2 ; -2) hoặc B(-2 ; -2), C(4 ; 0).
Bài 3: Cho ba điểm A(1 ; 2), B(-3 ; 1), C(4 ; -2).
a) Chứng minh rằng tập hợp các điểm M(x;y) thỏa mãn \(M{A^2} + M{B^2} = M{C^2}\) là một đường tròn.
Advertisements (Quảng cáo)
b) Tìm tọa độ tâm và bán kính của đường tròn nói trên.

a) \(M{A^2} + M{B^2} = M{C^2}\)
\( \Leftrightarrow {\left( {x – 1} \right)^2} + {\left( {y – 2} \right)^2} + {\left( {x + 3} \right)^2} + {\left( {y – 1} \right)^2} = {\left( {x – 4} \right)^2} + {\left( {y + 2} \right)^2}\)
\(\Leftrightarrow {x^2} + {y^2} + 12x – 10y – 5 = 0\)
\( \Leftrightarrow {\left( {x + 6} \right)^2} + {\left( {y – 5} \right)^2} = 66.\)
Vậy tập hợp các điểm M là một đường tròn.
b) Tâm là điểm (-6 ; 5) bán kính bằng \(\sqrt {66} \)
Bài 4: Cho hai điểm A(3 ; -1), B(-1 ; -2) và đường thẳng d có phương trình x + 2y + 1 = 0
a) Tìm tọa độ điểm C trên đường thẳng d sao cho tam giác ABC là tam giác cân tại C.
b) Tìm tọa độ điểm M trên đường thẳng d sao cho tam giác AMB vuông tại M.

a) Đặt C(x ; y), ta có : \(C \in d \Leftrightarrow x = – 2y – 1\). Vậy C( – 2y – 1;y).
Tam giác ABC cân tại C khi và chỉ khi
CA = CB \( \Leftrightarrow C{A^2} = C{B^2}\)
\( \Leftrightarrow {\left( {3 + 2y + 1} \right)^2} + {\left( { – 1 – y} \right)^2} = {\left( { – 1 + 2y + 1} \right)^2} + {\left( { – 2 – y} \right)^2}\)
\( \Leftrightarrow {\left( {4 + 2y} \right)^2} + {\left( {1 + y} \right)^2} = 4{y^2} + {\left( {2 + y} \right)^2}\)
Giải ra ta được \(y = – {{13} \over {14}}.\)
\(x = – 2\left( {{{ – 13} \over {14}}} \right) – 1 = {{13} \over 7} – 1 = {6 \over 7}.\)
Vậy C có tọa độ là \(\left( {{6 \over 7}; – {{13} \over {14}}} \right)\)
b) Xét điểm M( – 2t – 1;t) trên d, ta có :
\(\widehat {AMB} = {90^ \circ } \Leftrightarrow A{M^2} + B{M^2} = A{B^2}\)
\( \Leftrightarrow {\left( {4 + 2t} \right)^2} + {\left( {1 + t} \right)^2} + 4{t^2} + {\left( {2 + t} \right)^2} = 17\)
\( \Leftrightarrow 10{t^2} + 22t + 4 = 0 \Leftrightarrow 5{t^2} + 11t + 2 = 0\)
\( \Leftrightarrow \left[ \matrix{
t = – {1 \over 5} \hfill \cr
t = – 2. \hfill \cr} \right.\)
Vậy có hai điểm thỏa mãn đề bài là \({M_1}\left( { – {3 \over 5}; – {1 \over 5}} \right)\) và \({M_2}\left( {3; – 2} \right)\)

