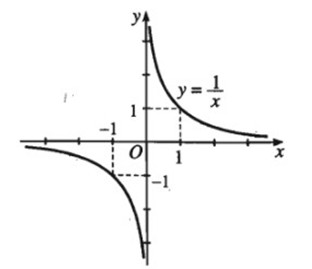
Bài 13: Hàm số \(y = {1 \over x}\) có đồ thị như hình 2.10
a) Dựa vào đồ thị, hãy lập bảng biến thiên của hàm số đó
b) Bằng tính toán, hãy khảo sát sự biến thiên của hàm số trên khoảng (-∞, 0) và (0, +∞) và kiểm tra lại kết quả so với bảng biến thiên đã lập
Giải
a) Bảng biến thiên của hàm số
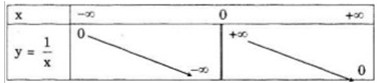
b) Với x1, x2 ∈ \((-∞; 0)\) và x1 ≠ x2; ta có:
\({{f({x_2}) – f({x_1})} \over {{x_2} – {x_1}}} = {{{1 \over {{x_2}}} – {1 \over {{x_1}}}} \over {{x_2} – {x_1}}} = {{ – 1} \over {{x_1}{x_2}}} < 0\) (vì x1 < 0; x2 < 0)
Vậy hàm số \(y = {1 \over x}\) nghịch biến trên \((-∞; 0)\)
Tương tự hàm số \(y = {1 \over x}\) cũng nghịch biến trên \((0; +∞)\)
Advertisements (Quảng cáo)
Bài 14: Tập con S của tập số thực \(\mathbb R\) gọi là đối xứng nếu mọi x thuộc S, ta đều có – x thuộc S. Em có nhận xét gì về tập xác định của một hàm số chẵn (lẻ).
Từ nhận xét đó, em có kết luận gì về tính chẵn – lẻ của hàm số \(y = \sqrt x \) ? Tại sao?
Tập xác định của một hàm số chẵn (lẻ) là tập đối xứng.
Hàm số \(y = \sqrt x \) không là hàm số chẵn, cũng không là hàm số lẻ vì tập xác định của nó là \(D = [0; +∞)\) không phải là tập đối xứng (do 1 ∈ D nhưng -1 ∉ D).
Bài 15: Gọi (d) là đường thẳng \(y = 2x\) và (d’) là đường thẳng \(y = 2x – 3\). Ta có thể coi (d’) có được là do tịnh tiến (d):
Advertisements (Quảng cáo)
a) Lên trên hay xuống dưới bao nhiêu đơn vị?
b) Sang trái hay sang phải bao nhiêu đơn vị?
a)
(d’) có được là do tịnh tiến xuống dưới 3 đơn vị
b) Ta có:
\(y = 2x – 3 = 2(x – {3 \over 2})\)
Vậy (d’) có được là do tịnh tiến (d) sang phải \({3 \over 2}\) đơn vị.
Bài 16: Cho đồ thị (H) của hàm số: \(y = – {2 \over x}\)
a) Tịnh tiến (H) lên trên 1 đơn vị, ta được đồ thị của hàm số nào ?
b) Tịnh tiến (H) sang trái 3 đơn vị, ta được đồ thị của hàm số nào?
c) Tịnh tiến (H) lên trên 1 đơn vị, sau đó tịnh tiến đồ thị nhận được sang trái 3 đơn vị, ta được đồ thị của hàm số nào ?
a) Tịnh tiến (H) lên trên 1 đơn vị, ta được đồ thị hàm số \(y = {{ – 2} \over x} + 1\)
b) Tịnh tiến (H) sang trái 3 đơn vị, ta được đồ thị hàm số \(y = – {2 \over {x + 3}}\)
c) Tịnh tiến (H) lên trên 1 đơn vị, sau đó tịnh tiến đồ thị nhận được sang trái 3 đơn vị, ta được đồ thị hàm số \(y = – {2 \over {x + 3}} + 1\)

