Bài 1: Tốc độ của chất điểm dao động điều hoà cực đại khi
A. Li độ cực đại. B. Gia tốc cực đại.
C. Li độ bằng \(0\). D. pha bằng \({\pi \over 4}\).
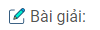
Tốc độ của chất điểm dao động điều hoà cực đại khi li độ bằng 0.
Chọn đáp án C.
Lưu ý : Giữa li độ và vận tốc v có công thức liên hệ:
\({\left( {{x \over A}} \right)^2} + \left( {{v \over {A\omega }}} \right)^2 = 1\)
\(\Rightarrow \) Khi \(x=0\) thì \(v = A\omega \) cực đại.
Bài 2: Gia tốc của chất điểm dao động điều hoà bằng 0 khi
A. Li độ cực đại.
B. Li độ cực tiểu.
C. Vận tốc cực đại hoặc cực tiểu.
D. Vận tốc bằng \(0\).
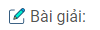
Gia tốc chất diểm dao động điều hoà bằng 0 khi vận tốc cực đại hoặc cực tiểu.
Chọn đáp án C.
Lưu ý : Khi vmax thì \(x = 0 \Rightarrow a = – {\omega ^2}x = 0.\)
vmin = 0 ở vị trí biên thì lúc đó \(a = v’ =0\).
Bài 3: Dao động điều hoà đổi chiều khi
A. Lực tác dụng đổi chiều.
B. Lực tác dụng bằng 0.
C. Lực tác dụng có độ lớn cực đại.
D. Lực tác dụng có độ lớn cực tiểu.
Advertisements (Quảng cáo)
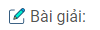
Dao động cơ điều hoà, đổi chiều khi lực tác dụng có độ lớn cực đại.
Chọn đáp án C.
Lưu ý : Lực phục hồi \(F = -kx\) lớn nhất khi vật ở vị trí biên Fmax = kA, lúc đó vật dao động đổi chiều để chuyển động ngược lại.
Bài 4: a) Thử lại rằng :\(x = {A_1}\cos \omega t + {A_2}\sin \omega t\) (6.14) trong đó A1 và A2 là hai hằng số bất kì cũng là nghiệm của phương trình (6.3).
b) Chứng tỏ rằng, nếu chọn A1 và A2 trong biểu thức ở vế trái của (6.14) như sau: \({A_1} = A\cos \varphi ;{A_2} = – A\sin \varphi \) thì biểu thức ấy trùng với biểu thức ở vế phải của (6.4).
a) Ta có :
\(x = {A_1}\cos \omega t + {A_2}\sin \omega t \)
\(\Rightarrow x’ = – {A_1}\omega \sin \omega t + {A_2}\omega \cos \omega t.\)
\(x” = – {A_1}{\omega ^2}\cos \omega t – {A_2}{\omega ^2}\sin \omega t.\)
Ta được :
\(\eqalign{
& x” + {\omega ^2}x = – {A_1}{\omega ^2}\cos \omega t – {A_2}{\omega ^2}sin\omega t + \cr&{\omega ^2}({A_1}\cos \omega t + {A_2}\sin \omega t) \cr
& \Rightarrow x” + {\omega ^2}x = – {A_1}{\omega ^2}\cos \omega t – {A_2}{\omega ^2}sin\omega t\cr& + {A_1}{\omega ^2}\cos \omega t + {A_2}{\omega ^2}sin\omega t = 0. \cr} \)
Vậy :\(x = {A_1}\cos \omega t + {A_2}\sin \omega t\) là nghiệm của phương trình \(x” + {\omega ^2}x = 0.\)
b) Nếu chọn \({A_1} = A\cos \varphi \) và \({A_2} = – A\sin \varphi \)
Advertisements (Quảng cáo)
thì
\(\eqalign{& x = {A_1}\cos \omega t + {A_2}\sin \omega t \cr&= A\cos \varphi cos\omega t – A\sin \varphi \sin \omega t \cr & = A(\cos \varphi cos\omega t – \sin \varphi \sin \omega t) \cr & \Rightarrow x = Acos\left( {\omega t + \varphi } \right). \cr} \)
Bài 5: Phương trình dao động của một vật là :\(x = 6\cos \left( {4\pi t + {\pi \over 6}} \right)(cm).\)
a) Xác định biên độ, tần số góc, chu kì và tần số của dao dộng.
b) Xác định pha của dao động tại thời điểm \(t = {1 \over 4}s\), từ đó suy ra li độ tại thời điểm ấy.
c) Vẽ vectơ quay biểu diễn dao động tại thời điểm \(t = 0\).
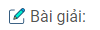
Phương trình dao động của vật :\(x = 6\cos \left( {4\pi t + {\pi \over 6}} \right)(cm)\)
a) Biên độ \(A =6\) (cm)
Chu kì \(T = {{2\pi } \over \omega } = {{2\pi } \over {4\pi }} = 0,5(s)\)
Tần só góc \(\omega = 4\pi (rad/s)\)
Tần số \(f = {1 \over T} = {1 \over {0,5}} = 2(Hz)\)
b) Khi \(t = {1 \over 4}(s) \Rightarrow pha\;(\omega t + \varphi ) = \left( {4\pi .{1 \over 4} + {\pi \over 6}} \right) = {{7\pi } \over 6}\)
\( \Rightarrow x = 6\cos \left( {\pi + {\pi \over 6}} \right) = – 6\cos {\pi \over 6} = – 6.{{\sqrt 3 } \over 2}\)
\(= – 3\sqrt 3 (cm).\)
c) Vẽ vectơ quay biểu diễn dao động vào thời điểm \(t =0\):
Bài 6: Một vật dao động điều hoà với biên độ \(A= 4\) cm và chu kì \(T = 2\) s.
a) Viết phương trình dao động của vật, chọn gốc thời gian là lúc nó đi qua vị trí cân bằng theo chiều dương.
b) Tính li độ của vật tại thời điểm \(t = 5,5\) s.
Giải
a) Vật dao động điều hoà với \(A = 4cm\), \(T = 2\) (s)
Tần số góc của dao động \(\omega = {{2\pi } \over T} = {{2\pi } \over 2} = \pi \,(rad/s)\)
Chọn gốc thời gian lúc vật qua vị trí cân bằng theo chiều dương
\( \Rightarrow \) Khi \(t = 0\) : \(\left\{ \matrix{{x_0} = A\cos \varphi = 0(1) \hfill \cr \hfill \cr {v_0} = – A\omega \sin \varphi > 0(2) \hfill \cr} \right.\)
\(\eqalign{& (1) \Rightarrow \cos \varphi = 0 \Rightarrow \left[ \matrix{\varphi = {\pi \over 2} \hfill \cr \varphi = – {\pi \over 2} \hfill \cr} \right. \cr & \cr} \)
\((2) \Rightarrow {v_0} > 0 \Leftrightarrow \sin \varphi < 0 \Rightarrow \) Chọn \(\varphi = – {\pi \over 2}.\)
Vậy : \(x = 4\cos \left( {\pi t – {\pi \over 2}} \right)(cm).\)
b) Khi \(t = 5,5\) (s), ta có
\(\eqalign{& x = 4\cos \left( {\pi .5,5 – {\pi \over 2}} \right) \cr & x = 4\cos 5\pi = – 4(cm). \cr} \)
Bài 7: Một vật nặng treo vào một lò xo làm cho nó dãn ra \(0,8\) cm. Cho vật dao động. Tìm chu kì dao động ấy. Lấy \(g = 10m/{s^2}\).
Giải
Khi treo vật vào lò xo làm lò xo dãn ra một đoạn \(\Delta \ell = 0,8(cm)\) ở vị trí cân bằng.
Theo định luật I Niutơn:
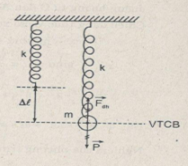
\(\eqalign{& \overrightarrow P + \overrightarrow {{F_{đh}}} = 0 \cr & \Leftrightarrow P = {F_{đh}} \cr & \Leftrightarrow mg = k\Delta \ell \cr & \Leftrightarrow {m \over k} = {{\Delta \ell } \over g} \cr} \)
Khi cho vật dao động, chu kì dao động của con lắc lò xo là
\(T= 2\pi \sqrt {{m \over k}} = 2\pi \sqrt {{{\Delta \ell } \over g}} = 2\pi \sqrt {{{0,{{8.10}^{ – 2}}} \over {10}}} = 0,18(s)\)

