Câu C1: Tìm mối liện hệ giữa dấu của công với chiều diễn biến của quá trình đẳng áp.Công trong quá trình đẳng áp
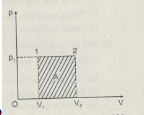
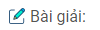
Nếu khí biến đổi từ trạng thái 1 sang trạng thái 2 khí dãn nở đẳng áp, sinh công (thực hiện công nên pit-tông đẩy nó lên) nên \({A’}\) mang dấu dương: \({A’}\) > 0.
Nếu theo chiều từ 2 sang 1 thì khí bị ném đẳng áp: nhận công từ vật khác \( \to {A’}\)< 0.
Câu C2: Tìm mỗi liên hệ giữa dấu của công A’ với chiều diễn biến của quả trình đẳng nhiệt.
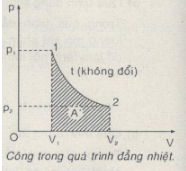
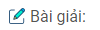
Quá trình từ 1 sang 2: khí dãn nở đẳng nhiệt, sinh công \(A’> 0\).
Quá trình từ 2 sang 1: khí bị nén đẳng nhiệt, nhận công \(A'< 0\).
Câu C3: Tìm mối liên hệ giữa dấu của công A’ do khí sinh ra với chiều diễn biến của chu trình.
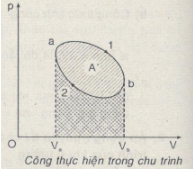
Nếu khí chuyển đổi theo chiều \(\overrightarrow {a1b2a} \) thì trong quá trình \(\overrightarrow {a1b} \) khí dãn nở sinh công \(\left| {{A_1}} \right|\) được biểu diễn bằng điện tích \({S_1}\) của hình \({V_{^{_a}}}a1b{V_b}\).
Trong quá trình \(\overrightarrow {b2a} \) khí dãn nở công \({A_2}\) được biểu diễn bằng diện tích \({S_2}\) của hình \({V_a}a2bV\) với \({S_2} < {S_1}\).
Vì vậy công chu trình \(\overrightarrow {a1b2a} :A’ = {A_1} + {A_2} > 0\).
Ngược lại, công của chu trình \(\overrightarrow {a2b1a} :{A_1} + {A_2} < 0\).
Advertisements (Quảng cáo)
Bài 1: Một lượng khí được dãn thể tích \({V_1}\) đến thể tích \({V_2}({V_2} > {V_1})\). Trong quá trình nào lượng khí thực hiện công ít nhất?
A.Trong quá trình nở đẳng áp.
B.Trong quá trình đẳng nhiệt.
C.Trong quá trình nở đẳng áp rồi dãn đẳng nhiệt.
D.Trong quá trình dãn đẳng nhiệt rồi nở đẳng áp.
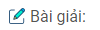
Chọn B. (Dựa vào diện tích gạch chéo trên đồ thị trong hệ p-V).
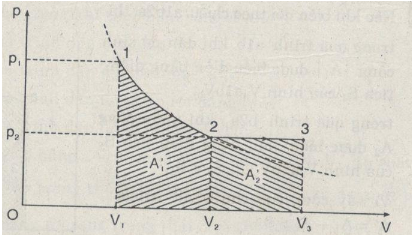
Bài 2: Một lượng khí không đổi ở trạng thái 1 thể tích \({v_1}\) , áp suất \({p_1} \) , dãn đẳng nhiệt đến trạng thái 2 có thể tích \({V_2} = 2{V_1}\) và áp suất \({p_2} = {{{p_1}} \over 2}\). sau đó dãn đẳng nhiệt sang trạng thái 3 có thể tích \({V_3} = 3{V_1}\).
Vẽ đồ thị biểu diễn các quá trình trên. Dùng đồ thị để so sánh công trong khí các quá trình trên
Advertisements (Quảng cáo)
Đồ thị biểu diễn quá trình từ 1 \(({V_1},{p_1},{T_1})\)
\( \Rightarrow 2({V_2} = 2{V_1};{p_2} = {{{p_1}} \over 2};{T_2} = {T_1})\)
\( \Rightarrow 3({V_3} = 3{V_1};{p_3} = {p_2};{T_3}).\)
\({S_{{V_1}12{V_2}}} > {S_{{V_2}23{V_3}}}\) nên \(A_1′ > A_2’\)
Công khí sinh ra trong quá trình \(1 \to 2\) lớn hơn công sinh ra trong quá trình \(2 \to 3\) .
Bài 3: Một lượng khí lí tưởng thể tích \({V_1}\) lít và áp suất \({p_1}\) atm được dãn đẳng nhiệt tới khi thể tích đạt giá trị \({V_2} = 2\) lít. Sau đó người ta làm lạnh khí, áp suất của khí giảm đi một nửa, còn thể tích thì không. Cuối cùng khí dãn đẳng áp tới thể tích đạt giá trị \({V_3} = 4\) lít.
Vẽ đồ thị biểu diễn các quá trình trên. Dùng đồ thị để so sánh công của khí trong quá trình trên.
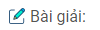
Đồ thị sự phụ thuộc p vào V
Diện tích \({S_{2344}} = {S_{12’22}} < {S_{1122}}\)
Bài 4: Lấy 2,5 mol khí lí tưởng ở nhiệt độ 300 K. Nung nóng đẳng áp lượng khí này cho đến khi thể tích của nó bằng 1,5 lần thể tích lúc đầu. nhiệt lượng cung cấp cho khí trong quá trình này là 11,04 kJ. Tính công mà khí thực hiện và độ tăng nội năng.
Áp định luật Gay Luy-xác, ta được:
\({{{V_1}} \over {{T_1}}} = {{{V_2}} \over {{T_2}}} \Rightarrow {T_2} = {{{V_2}} \over {{V_1}}}{T_1} = 1,5.300 = 450\) (k)
Áp dụng phương trình C – M
Cho trạng thái 1:\(p{V_1} = 2,5R{T_1}\)
Cho trạng thái 2:\(p{V_2} = 2,5R{T_2}\)
\( \Rightarrow p\left( {{V_2} – {V_1}} \right) = 2,5R\left( {{T_2} – {T_1}} \right)\)
Hay công của khí \({A’} = 2,5.8,31.(450 – 300) = 3,12\)(kJ)
Áp dụng nguyên lí I cho quá trình đẳng áp:
\(\Delta U = Q – {A’} = 11,04 – 3,12 = 7,92\) (kJ)

