Câu C1: Một vật được thả tự do từ độ cao h xuống đất. Hãy áp dụng định luật bảo toàn cơ năng để chứng tỏ rằng vận tốc của vật khi chạm đất là:
\(v = \sqrt {2gh} \)
Thế năng của vật trong trọng trường cũng có thể là thế năng của hệ vật-Trái Đất. Trong tương tác với vật, Trái Đất có khối lượng rất lớn nên coi như đứng yên (có động năng bằng 0). Vì lẽ đó cơ năng của hệ vật – Trái Đất cũng là cơ năng của vật trong trọng trường. Có thể phát biểu: “ Cơ năng của hệ vật- Trái Đất( hệ kín, tương tác bằng lực thế ) được bảo toàn”.
Chọn mức 0 thế năng tại mặt đất thì thế năng ở độ cao là Wt=mgh
Vật thả rơi tự do nên v0=0\( \Rightarrow \) động năng ở độ cao h : Wđ=0
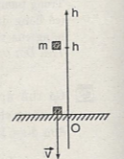
Gọi vận tốc chạm đất là v thì động năng trước khi chạm đất là Wđ=\({1 \over 2}m{v^2}\).
Áp dụng định luật bảo toàn cơ năng: ta có \({1 \over 2}m{v^2} = mgh \Rightarrow v = \sqrt {2gh} \)
Câu C2: Có thể áp dụng định luật bảo toàn cơ năng cho chuyển động của con lắc đơn (Hình 37.1) được không?
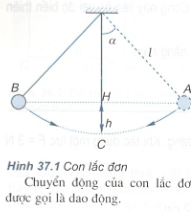
Nếu coi vật nặng (viên bi) chỉ chịu tác dụng của trọng lực thì có thể áp dụng định luật bảo toàn cơ năng cho chuyển động của con lắc đơn được: \({{\rm{W}}_A} = {{\rm{W}}_B} = {{\rm{W}}_C}\)
Bài 1: Một quả bóng được ném với vận tốc đầu xác định. Đại lượng nào không đổi khi quả bóng chuyển động?
A. Thế năng.
B. Động lượng.
C. Động năng.
Advertisements (Quảng cáo)
D. Gia tốc.
Chọn D.
Bài 2: Một hòn bi có khối lượng 20g được ném thẳng đứng lên cao với vận tốc 4m/s từ độ cao 1,6m so với mặt đất.
a) Tính trong hệ quy chiếu mặt đất các giá trị động năng, thế năng và cơ năng của hòn bi tại lúc ném vật.
b) Tìm độ cao cực đại mà bi đạt được.
a) Trong hệ quy chiếu mặt đất, lúc ném hòn bi có:
\(\eqalign{ & {{\rm{W}}_{{đ_1}}} = {{mv_1^2} \over 2} = {{0,{{02.4}^2}} \over 2} = 0,160(J); \cr & {{\rm{W}}_{{t_2}}} = mg{z_1} = 0,02.9,8.1,6 \approx 0,314(J) \cr & {{\rm{W}}_1} = {{\rm{W}}_{{{\rm{d}}_1}}} + {{\rm{W}}_{{t_1}}} = 0,16 + 0,31 = 0,474(J) \cr} \)
b) Áp dụng định luật bảo toàn cơ năng cho hai vị trí: vị trí ném và vị trí cao nhất (v2=0);
\({{\rm{W}}_2} = {{\rm{W}}_1} \Leftrightarrow mg{z_{{\rm{max}}}} = {{\rm{W}}_1} \)
Advertisements (Quảng cáo)
\(\Rightarrow {z_{\max }} = {{{{\rm{W}}_1}} \over {mg}} = {{0,474} \over {0,02.9,8}} \approx 2,42(m)\)
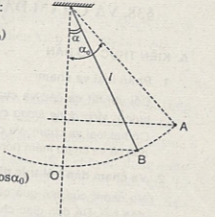
Bài 3: Một con lắc đơn có chiều dài l=1m. Kéo cho dây làm với phương thẳng đứng góc \(\alpha = {45^0}\) rồi thả tự do.Tìm vận tốc của con lắc khi nó đi qua:
a) vị trí ứng với góc 300;
b) vị trí cân bằng.
Chọn \({{\rm{W}}_{{t_0}}} = 0\) thì cơ năng tại \(A({\alpha _0})\) là :
\({\rm{W}} = {{\rm{W}}_{{t_A}}} = mg{z_A} = mg(l – l\cos {\alpha _0})\)
Thế năng tại \(B(\alpha ):{{\rm{W}}_t} = mgl(1 – \cos \alpha )\)
Động năng tại B: \({{\rm{W}}_đ} = {{m{v^2}} \over 2}\)
Áp dụng định luật bảo toàn cơ năng:
\(\eqalign{ & {{\rm{W}}_B} = {{\rm{W}}_A} \Leftrightarrow {{\rm{W}}_t} + {{\rm{W}}_đ} = {\rm{W}} \cr & \Leftrightarrow mgl(l – \cos \alpha ) + {{m{v^2}} \over 2} = mgl(1 – \cos {\alpha _0}) \cr & v = \sqrt {2gl(cos\alpha – \cos {\alpha _0})} \cr} \)
\(\eqalign{ & a)\alpha = {30^0} \Rightarrow v = \sqrt {2.9,8.1\left( {{{\sqrt 3 } \over 2} – {{\sqrt 2 } \over 2}} \right)} \cr& \approx 1,76(m/s) \cr & b)\alpha = {0^0} \Rightarrow v = \sqrt {2.9,8.2\left( {1 – {{\sqrt 2 } \over 2}} \right)} \cr& \approx 2,40(m/s) \cr} \)
Bài 4: Một vật được ném từ mặt đất với vận tốc 10m/s hướng chếch lên phía trên, với các góc ném hợp với phương ngang lần lượt là 300 và 600. Bỏ qua sức cản của không khí.
a) Vận tốc chạm đất của vật trong mỗi lần ném thay đổi ra sao?
b) Độ cao cực đại mà vật đạt được trong mỗi trường hợp bằng bao nhiêu?
Dùng định luật bảo toàn cơ năng để giải, có kết hợp với phương pháp động lực học.
a) Coi mặt đất là mặt phẳng ngang. Chọn Wt=0 tại mặt đất. Bỏ qua lực cản không khí thì cơ năng được bảo toàn, suy ra:
\({{\rm{W}}_{{đ_2}}} = {{\rm{W}}_{{đ_1}}} = {{\rm{W}}_{{đ_0}}}\) hay \({v_2} = {v_1} = {v_0} = 10(m/s)\)
Trong cả hai trường hợp với vận tốc chạm đất của vật đều có độ lớn bằng vận tốc ném nhưng khác nhau ở góc rơi \(\left\{ \matrix{ {\beta _1} = {\alpha _1} = {30^0} \hfill \cr {\beta _2} = {\alpha _2} = {60^0} \hfill \cr} \right.\)
b) Khi đạt độ cao cực đại thì vật có: \(v = {v_x} = {v_0}\cos \alpha .\)
Áp dụng định luật bảo toàn cơ năng :
\(\eqalign{ & mg{z_{\max }} + {1 \over 2}m{({v_0}\cos \alpha )^2} = {1 \over 2}(mv_0^2) \cr & {z_{\max }} = {{{{\left( {{v_0}\sin \alpha } \right)}^2}} \over {2g}} \cr} \)
Với \({\alpha _1} = {30^0}\) thì \({z_{1\max }} = {{{{\left( {10.0,5} \right)}^2}} \over {2.9,8}} \approx 1,28(m)\)
Với \(\alpha = {60^0}\) thì \({z_{2\max }} = {{{{\left( {10.{{\sqrt 3 } \over 2}} \right)}^2}} \over {2.9,8}} \approx 3,83(m).\)
