Câu 23. Cho hai đường thẳng a và b cùng song song với mp(P). Mệnh đề nào đúng trong các mệnh đề sau ?
a. a và b song song với nhau
b. a và b chéo nhau
c. a và b có thể cắt nhau
d. a và b trùng nhau
e. Các mệnh đề a), b), c), d) đều sai.
Mệnh đề c đúng.
Câu 24. Cho mp(P) và hai đường thẳng song song a, b. Mệnh đề nào đúng trong các mệnh đề sau đây ?
a. Nếu (P) song song với a thì (P) cũng song song với b
b. Nếu (P) song song với a thì (P) song song với b hoặc chứa b
c. Nếu (P) song song với a thì (P) chứa b
d. Nếu (P) cắt a thì (P) cũng cắt b
e. Nếu (P) cắt a thì (P) có thể song song với b
f. Nếu (P) chứa a thì (P) có thể song song với b
Mệnh đề a sai vì có thể b ⊂ (P)
Mệnh đề b đúng
Mệnh đề c sai vì có thể b // (P)
Mệnh đề d đúng
Mệnh đề e sai vì b cắt (P)
Mệnh đề f đúng
Câu 25. Cho hình tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC
Advertisements (Quảng cáo)
a. Xét vị trí tương đối của đường thẳng MN và mp(BCD)
b. Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC)
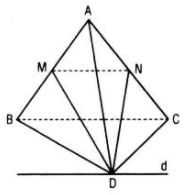
a. MN là đường trung bình của tam giác ABC nên MN // BC
Suy ra: MN // mp(BCD) (vì MN \( \not\subset \) (BCD))
b. Vì MN // (BCD) nên mp(DMN) đi qua MN cắt mp(BCD) theo giao tuyến d // MN.
Do đó d // mp(ABC)
Câu 26. khi cắt tứ diện bằng một mặt phẳng thì thiết diện nhận được có thể là những hình nào sau đây ?
a. Hình thang
b. Hình bình hành
c. Hình thoi
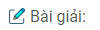
a.
Advertisements (Quảng cáo)
Có thể cắt tứ diện bằng một mặt phẳng để thiết diện là hình thang, ví dụ như mặt phẳng đi qua M, N (M, N là hai điểm lần lượt nằm trên hai cạnh AB, BC) và song song với BD
b.
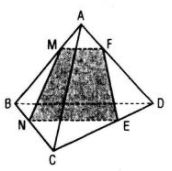
Có thể cắt tứ diện bằng một mặt phẳng để thiết diện là hình bình hành, ví dụ như mặt phẳng đi qua điểm M nằm trên cạnh AB và song song với hai đường thẳng BD và AC.
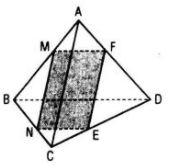
c. Có thể. Giả sử mặt phẳng cắt là (P) qua điểm M thuộc đoạn AB, song song với BD và AC. Khi đó thiết diện là hình bình hành MNEF.
Ta có:
\(\eqalign{ & {{MF} \over {BD}} = {{AM} \over {AB}} \Rightarrow MF = {{BD.AM} \over {AB}} \cr & {{MN} \over {AC}} = {{MB} \over {AB}} \Rightarrow MN = {{AC.MB} \over {AB}} \cr} \)
Tứ giác MNEF là hình thoi
\( \Leftrightarrow MF = MN \Leftrightarrow BD.AM = AC.MB \)
\(\Leftrightarrow {{AM} \over {MB}} = {{AC} \over {BD}}.\left( * \right)\)
Vậy với M xác định ở (*) thì mp(P) qua M và song song với AC, BD sẽ cắt tứ diện theo một thiết diện là hình thoi.
Câu 27. Cho hình chóp S.ABCD có đáy là tứ giác lồi, O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì ?
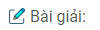
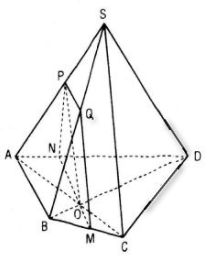
Gọi (α) là mặt phẳng qua O song song với AB và SC.
AB // (α) nên (α) cắt mp(ABCD) theo giao tuyến qua O và song song với AB. Gọi M, N lần lượt là giao điểm của đường thẳng qua O song song AB với BC và AD.
Trong mặt phẳng (SAC) kẻ OP // SC (P ϵ AS) (α) cắt mp(SAB) theo giao tuyến PQ // AB (Q ϵ SB)
Thiết diện cần tìm là tứ giác MNPQ.
Tứ giác MNPQ có PQ // MN nên MNPQ là hình thang.
Câu 28. Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA
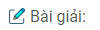
Gọi (β) là mặt phẳng qua M và song song với BD, SA.
BD // (β) nên (β) cắt mp(ABCD) theo giao tuyến MN // BD (N \(\in\) AD).
SA // (β) nên (β) cắt mp(SAB) theo giao tuyến MP // SA (P \(\in\) SB).
(β) cắt mp(SAD) theo giao tuyến NQ // SA (Q \(\in\) SD ).
Gọi {I} = MN ∩ AC.
(β) cắt mp(SAC) theo giao tuyến IK // SA (K \(\in\) SC)
Thiết diện cần tìm là ngũ giác MNQKP.

