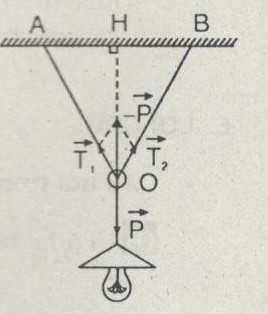
Câu C1: Trọng tâm O của vòng nhẫn ở đâu ?
Giải :
Trọng tâm G của vòng nhẫn trùng với tâm O của vòng nhẫn.
Bài 1: Điều kiện nào sau đây là đủ để hệ ba lực tác dụng lên cùng một vật rắn là cân bằng ?
A. Ba lực đồng quy.
B. Ba lực đồng phẳng.
C. Ba lực đồng phẳng và đồng quy.
D. Hợp lực của hai trong ba lực cân bằng với lực thứ ba.
Giải :
Chọn D
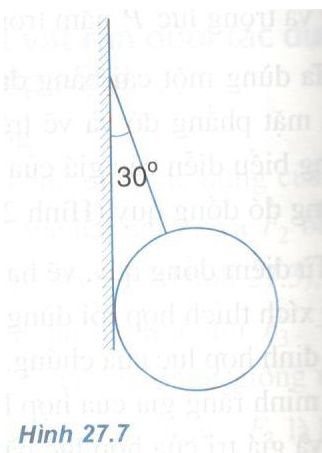
Bài 2: Một quả cầu có trọng lượng P = 40 N được treo vào tường nhờ một sợi dây hợp với mặt tường một góc \(\alpha = {30^0}\). Bỏ qua ma sát ở chỗ tiếp xúc giữa quả cầu và tường. Hãy xác định lực căng của dây và phản lực của tường tác dụng lên quả cầu (Hình 27.7).
Advertisements (Quảng cáo)
Giải :
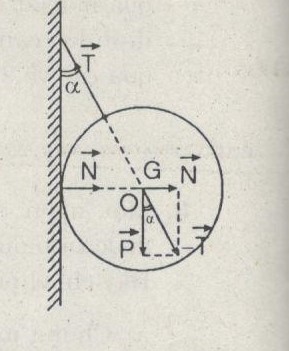
P = 40 N ; α = 300, bỏ qua ma sát phản lực \(\overrightarrow N \) của tường tác dụng lên cầu đặt tại tiếp điểm, vuông góc với tường (mặt phẳng tiếp tuyến) nên có giá qua tâm cầu.
Vậy quả cầu là vật rắn chịu tác dụng của ba lực đồng quy tại tâm cầu (O).
Điều kiện cân bằng của quả cầu :
\(\overrightarrow P + \overrightarrow N + \overrightarrow T = \overrightarrow 0 \,hay\,\overrightarrow P + \overrightarrow N = – \overrightarrow T \) (hình vẽ).
Từ hình vẽ, ta có: \(N = P\tan\alpha = P\tan{30^0} = 40.{1 \over {\sqrt 3 }} \approx 23,1(N)\)
Lực căng dây treo: \(T = {P \over {{\rm{cos}}\alpha }} = {{40} \over {{{\sqrt 3 } \over 2}}} = {{80} \over {\sqrt 3 }} \approx 46,2(N)\)
Advertisements (Quảng cáo)
Bài 3: Một ngọn đèn có khối lượng m = 1 kg được treo dưới trần nhà bằng một sợi dây. Dây chỉ chịu được lực căng lớn nhất 8 N.
a) Chứng minh rằng không thể treo ngọn đèn này vào đầu dây.
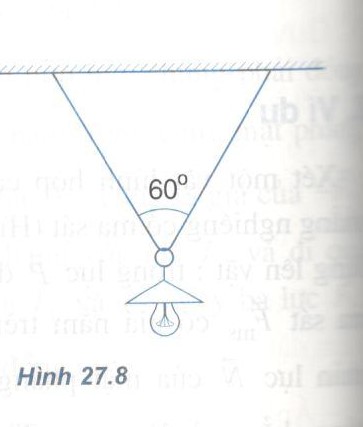
b) Người ta đã treo đèn này bằng cách luồn sợi dây qua một cái móc của đèn và hai đầu dây được gắn chặt trên trần nhà ( Hình 27.8) . Hai nửa sợi dây có chiều dài bằng nhau và hợp với nhau một góc bằng600. Hỏi lực căng của mỗi nửa sợi dây là bao nhiêu ?
Giải
a) Nếu treo đèn bằng 1 đầu dây thì khi cân bằng :
T = P = mg =1.9,8 = 9,8 N > TM = 8 N
Lực này vượt quá sức chịu đựng của dây nên dây sẽ đứt.
b) Nếu treo đèn bằng hai đầu dây như H.27.8 thì vòng móc treo đèn là vật rắn cân bằng dưới tác dụng của ba lực đồng quy tại tâm O của vòng : \(\overrightarrow P ;\overrightarrow {{T_1}} ;\overrightarrow {{T_2}} \).
Do đó có :
\(\overrightarrow {{T_1}} + \overrightarrow {{T_2}} = – \overrightarrow P \text{ với góc }\left( {\overrightarrow {{T_1}} ,\overrightarrow {{T_2}} } \right) = \widehat {AOB} = {60^0}.\)
Vì giá \(\overrightarrow P \) thẳng đứng, trần nhà AB ngang nên \(OH \bot AB\)
\(=>\) ∆OAB đều có OH là phân giác
\(=>\) hình bình hành là hình thoi có \(\widehat {AOH} = \widehat {BOH} = {30^0}\).
\( = > {T_1} = {T_2} = {P \over {2.c{\rm{os3}}{{\rm{0}}^0}}} = {{9,8} \over {2.{{\sqrt 3 } \over 2}}} \approx 5,66(N)\)