Bài 1: Xét dao động tổng hợp của hai dao động hợp thành có cùng phương và cùng tần số. Biên độ của dao động tổng hợp không phụ thuộc
A. Biên độ của dao động hợp thành thứ nhất.
B. Biên độ của dao động hợp thành thứ hai.
C. Tần số chung của hai dao động hợp thành.
D. Độ lệch pha của hai dao động hợp thành.
Từ biểu thức \({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos ({\varphi _2} – {\varphi _1})\).
Chọn đáp án C.
Bài 2: Hai dao động cơ điều hoà cùng phương, cùng tần số góc \(\omega = 50\;rad/s\), có biên độ lần lượt là \(100\; mm\) và \(173\; mm\), dao động thứ hai trễ pha \({\pi \over 2}\) so với dao động thứ nhất. Xác định dao động tổng hợp.
Hướng dẫn : Có thể chọn gốc thời gian so với pha ban đầu của dao động thứ nhất bằng \(0\).
Advertisements (Quảng cáo)
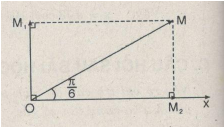
Chọn gốc thời gian sao cho pha ban đầu của dao động thứ hai bằng \(0\) thì dao động thứ nhất sẽ sớm pha hơn dao động thứ hai một góc \({\pi \over 2}\).
Suy ra :\({x_1} = 100\cos \left( {50t + {\pi \over 2}} \right)(mm);{x_2} = 173\cos 50t(mm)\)
Ta có thể giải bằng phương pháp vectơ quay.
\(\eqalign{
& OM = \sqrt {OM_1^2 + OM_2^2} \cr
& = \sqrt {{{100}^2} + {{173}^2}} \approx 200(mm) \cr
& \tan \varphi = {{O{M_1}} \over {O{M_2}}} = {{100} \over {173}} =0,578 \Rightarrow \varphi = {\pi \over 6} \cr} \)
Vậy \(x = 200\cos \left( {50t + {\pi \over 6}} \right)(mm)\)
Advertisements (Quảng cáo)
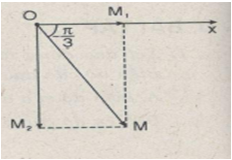
Cách khác : Ta có thể cho dao động thứ hai trễ pha \({\pi \over 2}\) so với dao động thứ nhất 1 góc \({\pi \over 2}\) thì :
\(\eqalign{
& {x_1} = 100\cos 50t(mm);{x_2} = 173\cos \left( {50t – {\pi \over 2}} \right)(mm) \cr
& OM = \sqrt {OM_1^2 + OM_2^2} = 200(mm) \cr} \)
Và \(\tan \varphi = – {{O{M_2}} \over {O{M_1}}} = – 1,73\Rightarrow \varphi = – {\pi \over 3}.\)
Vậy : \(x = 200\cos \left( {50t – {\pi \over 3}} \right)(mm)\)
Bài 3: Dùng công thức lượng giác (tổng của hai cosin) tìm tổng hợp của hai dao động điều hoà cùng phương, cùng tần số góc \(\omega \), cùng biên độ A và có độ lệch pha \(\Delta \varphi \). Đối chiếu với kết quả nhận được bằng phương pháp sử dụng giản đồ Fre – nen.
Tổng của hai dao động của hai dao động điều hoà cùng phương, cùng tần số góc \(\omega \), cùng biên độ A và có độ lệch pha \(\Delta \varphi = {\varphi _2} – {\varphi _1}.\)
\(\eqalign{
& {x_1} = A\cos (\omega t + {\varphi _1});{x_2} = A\cos (\omega t + {\varphi _2}). \cr
& \Rightarrow x = {x_1} + {x_2} = A\cos (\omega t + {\varphi _1}) + A\cos (\omega t + {\varphi _2}). \cr
& = A\left[ {\cos (\omega t + {\varphi _1}) + \cos (\omega t + {\varphi _2})} \right]. \cr
& = 2A\cos {{\omega t + {\varphi _1} + \omega t + {\varphi _2}} \over 2}\cos {{\omega t + {\varphi _1} – \omega t – {\varphi _2}} \over 2} \cr
& = 2A\cos {{2\omega t + {\varphi _1} + {\varphi _2}} \over 2}\cos {{{\varphi _1} – {\varphi _2}} \over 2} \cr
& x = 2A\cos {{\Delta \varphi } \over 2}\cos \left( {\omega t + {{{\varphi _1} + {\varphi _2}} \over 2}} \right). \cr} \)
+) Biên độ của dao động tổng hợp là \(2A\cos {{\Delta \varphi } \over 2}\)
+) Pha ban đầu của dao động tổng hợp : \(\varphi = {{{\varphi _1} + {\varphi _2}} \over 2}\)
* Nếu dùng phương pháp giản đồ Fre-nen thì :
\(\eqalign{
& {A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}\cos \left( {{\varphi _1} – {\varphi _2}} \right) \cr
& = {A^2} + {A^2} + 2{A^2}\cos \Delta \varphi = 2{A^2}(1 + \cos \Delta \varphi ) \cr
& = 2{A^2}.2{\cos ^2}{{\Delta \varphi } \over 2} = 4{A^2}{\cos ^2}{{\Delta \varphi } \over 2}. \cr
& \Rightarrow A = 2A\cos {{\Delta \varphi } \over 2}. \cr
& \tan \varphi = {{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}} \over {{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}} = {{A\sin {\varphi _1} + A\sin {\varphi _2}} \over {A\cos {\varphi _1} + A\cos {\varphi _2}}} \cr
& {{\sin {\varphi _1} + \sin {\varphi _2}} \over {\cos {\varphi _1} + \cos {\varphi _2}}} = {{2\sin {{{\varphi _1} + {\varphi _2}} \over 2}\cos {{{\varphi _1} – {\varphi _2}} \over 2}} \over {2\cos {{\varphi _1^{} + {\varphi _2}} \over 2}\cos {{{\varphi _1} – {\varphi _2}} \over 2}}} = \tan {{{\varphi _1} + {\varphi _2}} \over 2} \cr
& \Rightarrow \varphi = {{{\varphi _1} + {\varphi _2}} \over 2}. \cr} \)

