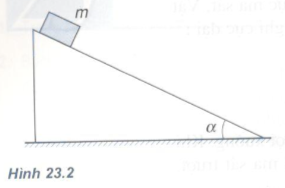
Bài 1: Vật khối lượng m đặt trên mặt phẳng nghiêng hợp với phương nằm ngang một góc α (Hình 23.2). Hệ số ma sát trượt giữa vật và mặt phẳng nghiêng là \({\mu _t}\). Khi được thả ra, vật trượt xuống. Gia tốc của vật phụ thuộc vào những đại lượng nào ?
A. \({\mu _t}\), m, α B. \({\mu _t},g,\alpha \)
C. \(m,\,g,\,{\mu _t}\) D. \(m,\,g,\,{\mu _t},\alpha \)
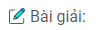
Chọn B (Hiểu từ biểu thức tính gia tốc \(a = g(\sin \alpha – {\mu _t}{\rm{cos}}\alpha {\rm{)}}\).
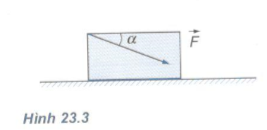
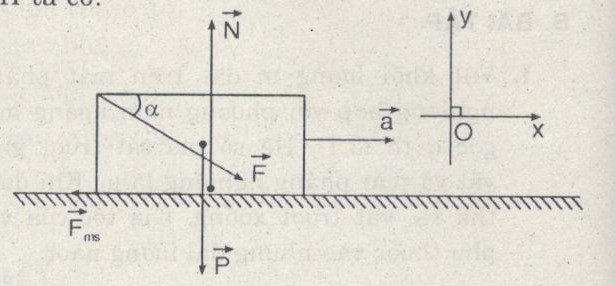
Bài 2: Một cái hòm khối lượng m = 40 kg đặt trên sàn nhà. Hệ số ma sát trượt giữa hòm và sàn nhà là \({\mu _t} = 0,2\). Người ta đẩy hòm bằng một lực F =200N theo phương hợp với phương nằm ngang một góc \(\alpha = {30^0}\), chếch xuống phía dưới (Hình 23.3). Tính gia tốc của hòm.
Giải
\(m = 40\,kg\,;\alpha = {30^0};{\mu _t} = 0,2\,;\)
\(F = 200\,N;g = 9,8(m/{s^2})\)
Vật chịu tác dụng của 4 lực được biểu diễn như hình vẽ.
Áp dụng định luật Niu -tơn II ta có :
\(\overrightarrow a = {{\overrightarrow P + \overrightarrow N + \overrightarrow F + \overrightarrow {{F_{msn}}} } \over m}(1)\)
Chiếu (1) lên trục Oy được :
\(\eqalign{ & 0 = {{ – P + N – F\sin \alpha } \over m} \cr & N = mg + F\sin \alpha \cr & \,\,\,\, = 40.9,8 + 200.0,5 = 492(N) \cr & {F_{ms}} = {\mu _t}N = 0,2.492 = 98,4(N) \cr} \)
Advertisements (Quảng cáo)
Chiếu (1) lên Ox được :
\(a = {{{F}{\rm{cos}}\alpha – {F_{ms}}} \over m} = {{200{{\sqrt 3 } \over 2} – 98,4} \over {40}} = 1,87(m/{s^2})\)
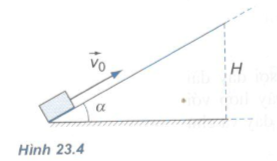
Bài 3: Một vật đặt trên mặt phẳng nghiêng (góc nghiêng α = 300) , được truyền một vận tốc ban đầu \({v_0} = 2m/s\)(Hình 23.4). Hệ số ma sát giữa vật và mặt phẳng nghiêng là 0,3.
a) Tính gia tốc của vật.
b) Tính độ cao lớn nhất (H) mà vật đạt tới.
c) Sau khi đạt tới độ cao H, vật sẽ chuyển động như thế nào ?
Giải
Advertisements (Quảng cáo)
\(\alpha = {30^0}\,;{v_0} = 2m/s;{\mu _t} = 0,3\)
Chọn gốc tọa độ O là điểm truyền vận tốc v0, chiều trục như hình vẽ.
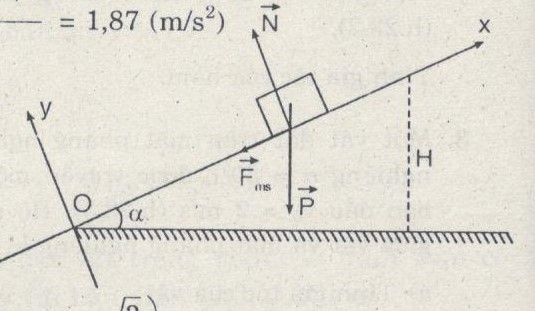
a) Gia tốc của vật:
\(\eqalign{ & a = – g\left( {\sin \alpha + {\mu _t}{\rm{cos}}\alpha } \right) = – 9,8\left( {0,5 + 0,3{{\sqrt 3 } \over 2}} \right) \cr & a = – 7,45(m/{s^2}) \cr} \)
b) Khi đạt độ cao cực đại thì vật có v = 0 nên quãng đường đi được tới lúc đó là
\(\eqalign{ & S = {{ – v_0^2} \over {2a}} \cr & \,{H_{\max }} = S.\sin \alpha = {{ – {v_0}^2\sin \alpha } \over {2a}} = {{ – {2^2}.0,5} \over {2.( – 7,45)}}\cr&\;\;\;\;\;\;\;\;\;\;\; \approx 0,134(m) = 13,4cm \cr} \).
c) Coi \({\mu _n} = {\mu _t} = 0,3\). Tại vị trí cao nhất, lực ma sát chuyển thành ma sát nghỉ, chiều dương hướng lên.
So sánh hai thành phần lực Px và Fmsn ta thấy:
\({{{P_x}} \over {{F_{ms}}}} = {{mg\sin \alpha } \over {{\mu _n}mg\cos \alpha }}\, = {{\tan \alpha } \over {{\mu _n}}}\, = {1 \over {0,3\sqrt 3 }} > 1\)
Vậy vật đổi chiều chuyển động, chuyển động nhanh dần đều xuống với gia tốc khác:
\({a’} = – g(\sin \alpha – {\mu _t}{\rm{cos}}\alpha {\rm{)}} \approx {\rm{ – 0,19(m/}}{{\rm{s}}^2})\)
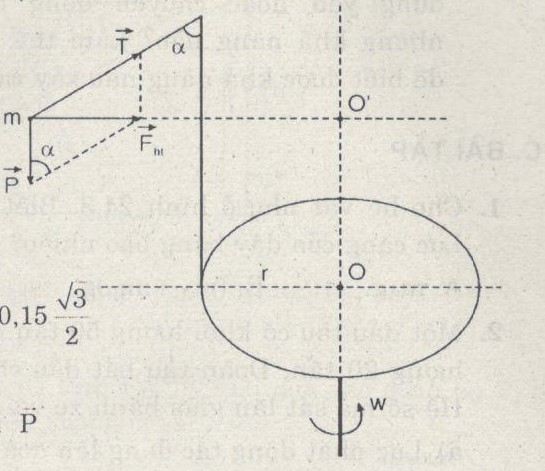
Bài 4: Một con lắc gồm một quả cầu nhỏ khối lượng m = 200 g treo vào sợi dây chiều dài l = 15 cm, buộc vào đầu một cái cọc gắn với mép một cái bàn quay (Hình 23.5). Bàn có bán kính r = 20 cm và quay với vận tốc không đổi.
a) Tính số vòng quay của bàn trog 1 min để dây nghiêng so với phương thẳng đứng một góc \(\alpha = {60^0}\).
b) Tính lực căng của dây trong trường hợp của câu a).
Giải
a) Khi bàn quay đều với vận tốc góc \(\omega \) thì chất điểm m chuyển động tròn đều trên một đường tròn nằm ngang tâm O’.
Bán kính quỹ đạo:
\(\eqalign{ & R = r + l\sin \alpha = 0,2 + 0,15{{\sqrt 3 } \over 2} \cr & R \approx 0,33\,m \cr} \)
Lực hướng tâm là hợp của \(\overrightarrow P \,và\,\overrightarrow T \,nên\,\overrightarrow {{F_{ht}}} = \overrightarrow P + \overrightarrow T \)
\(\eqalign{ & = > {F_{ht}} = P.\tan \alpha < = > mR{\omega ^2} = mg.\tan \alpha \cr& < = > R{(2\pi f)^2} = g\tan \alpha \cr & = > f = {1 \over {2\pi }}\sqrt {{{g\tan \alpha } \over R}} = {1 \over {2.3,14}}.\sqrt {{{9,8.\sqrt 3 } \over {0,33}}} \cr&\;\;\;\;\;\;\;\;\;\;=1,142\;Hz \cr} \)
Số vòng quay trong 1 min: \(n = 60f = 68,5\) (v/min)
b) Lực căng dây: \(T = {P \over {{\rm{cos}}\alpha }} = {{mg} \over {{\rm{cos}}\alpha }} = {{0,2.9,8} \over {0,5}} = 3,92(N)\)