Bài 9: Tìm tập xác định của mỗi hàm số sau:
a) \(y = {{3x + 1} \over {{x^2} – 9}}\)
b) \(y = {x \over {1 – {x^2}}} – \sqrt { – x} \)
c) \(y = {{x – 3\sqrt {2-x} } \over {\sqrt {x + 2} }}\)
d) \(y = {{\sqrt {x – 1} + \sqrt {4 – x} } \over {(x – 2)(x – 3)}}\)
a) y xác định \( \Leftrightarrow {\rm{ }}{x^2}-{\rm{ }}9{\rm{ }} \ne {\rm{ }}0{\rm{ }} \Leftrightarrow {\rm{ }}x{\rm{ }} \ne {\rm{ }} \pm {\rm{ }}3\)
Vậy tập xác định \(D = \mathbb R\backslash \left\{ { \pm {\rm{ }}3} \right\}\)
b)
y xác định
\( \Leftrightarrow \left\{ \matrix{
1 – {x^2} \ne 0 \hfill \cr
– x \ge 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ne \pm 1 \hfill \cr
x \le 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ne – 1 \hfill \cr
x \le 0 \hfill \cr} \right.\)
Vậy \(D = (-∞;-1)\cup (-1; 0]\)
c)
y xác định
\( \Leftrightarrow \left\{ \matrix{
2 – x \ge 0 \hfill \cr
x + 2 > 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \le 2 \hfill \cr
x > – 2 \hfill \cr} \right. \Leftrightarrow – 2 < x \le 2\)
Vậy \(D = (-2, 2]\)
d)
y xác định
\( \Leftrightarrow \left\{ \matrix{
x – 1 \ge 0 \hfill \cr
4 – x \ge 0 \hfill \cr
(x – 2)(x – 3) \ne 0 \hfill \cr} \right. \Leftrightarrow \left\{ \matrix{
x \ge 1 \hfill \cr
x \le 4 \hfill \cr
x \ne 2;\,x \ne 3 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
1 \le x \le 4 \hfill \cr
x \ne 2;x \ne 3 \hfill \cr} \right.\)
Vậy \( D = [1, 2) ∪(2, 3) ∪ (3, 4]\)
Bài 10: Cho hàm số:
\(f(x) = \left\{ \matrix{
– 2(x – 2);\,\,\, – 1 \le x < 1 \hfill \cr
\sqrt {{x^2} – 1} ;\,\,\,\,x \ge 1 \hfill \cr} \right.\)
a) Cho biết tập xác định của hàm số f
Advertisements (Quảng cáo)
b) Tính \(f(-1); f(0,5); f({{\sqrt 2 } \over 2} ); f(1); f(2)\)
a) Tập xác định của f là \(D = [-1, +∞)\)
b) Ta có:
\(f(-1) = -2(-1 – 2) = 6\)
\(f(0,5) = -2(0,5 – 2) = 3\)
\(f({{\sqrt 2 } \over 2}) = – 2({{\sqrt 2 } \over 2} – 2) = – \sqrt 2 + 4\)
\(f(1) = 0\)
\(f(2) =\sqrt 3\)
Bài 11: Trong các điểm \(A(-2, 8); B(4, 12); C(2, 8); D(5, 25 +\sqrt 2 )\)
Điểm nào thuộc, điểm nào không thuộc đồ thị của hàm số \(f(x) = {x^2} + \sqrt {x – 3} \) ? Vì sao?
Tập xác định của hàm số \(D = [3; +∞)\)
Ta có:
Advertisements (Quảng cáo)
\(x = -2\) và \(x = 2\) không thuộc tập xác định nên điểm \(A(-2; 8)\) và \(C(2; 8)\) không thuộc đồ thị hàm số.
Ta có:
\(f(4) = {4^2} + \sqrt {4 – 3} = 17\) \(⇒ B(4; 12)\) không thuộc đồ thị hàm số
\(f(5) = {5^2} + \sqrt {5 – 3} = 25 + \sqrt 2 \) \(⇒ D(5; 25 +\sqrt 2 )\) thuộc đồ thị hàm số
Bài 12: Khảo sát sự biến thiên của các hàm số sau
a) \(y = {1 \over {x – 2}}\) trên mỗi khoảng \((-∞; 2)\) và \((2; +∞)\)
b) y = x2 – 6x + 5 trên mỗi khoảng \((-∞; 3)\) và \((3; +∞)\)
c) y = x2005 + 1 trênn khoảng \((-∞; +∞)\)
a) \(f(x) = {1 \over {x – 2}}\)
+ Với x1; x2 ∈ \((-∞; 2)\) và x1 ≠ x2; ta có:
\(f({x_2}) – f({x_1}) = {1 \over {{x_2} – 2}} – {1 \over {{x_1} – 2}} = {{{x_1} – 2 – {x_2} + 2} \over {({x_1} – 2)({x_2} – 2)}}\)
\(= {{{x_1} – {x_2}} \over {({x_1} – 2)({x_2} – 2)}}\)
\( \Rightarrow {{f({x_2}) – f({x_1})} \over {{x_2} – {x_1}}} = {{ – 1} \over {({x_1} – 2)({x_2} – 2)}} < 0\)
Vậy hàm số \(y = {1 \over {x – 2}}\) nghịch biến trên \((-∞; 2)\)
+ Với x1; x2 ∈ \((2; +∞)\) và x1 ≠ x2; ta có:
\({{f({x_2}) – f({x_1})} \over {{x_2} – {x_1}}} = {{ – 1} \over {({x_1} – 2)({x_2} – 2)}} < 0\)
Vậy hàm số \(y = {1 \over {x – 2}}\) nghịch biến trên \((2; +∞)\)
Bảng biến thiên
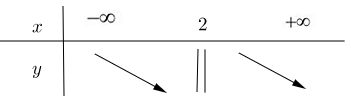
b) f(x) = x2 – 6x + 5
+ Với x1; x2 ∈ \((-∞; 3)\) và x1 ≠ x2; ta có:
f(x2) – f(x1) = x22 – 6x2 + 5 – (x12 – 6x1 + 5)
= x22 – x12 + 6(x1 – x2) = (x2 – x1)(x1 + x2 – 6)
\( \Rightarrow {{f({x_2}) – f({x_1})} \over {{x_2} – {x_1}}} = {x_1} + {x_2} – 6 < 0\) (vì x1 < 3; x2 < 3)
Vậy hàm số y = x2 – 6x + 5 nghịch biến trên \((-∞, 3)\)
+ Với x1; x2 ∈ \((3, +∞)\) và x1 ≠ x2; ta có:
\({{f({x_2}) – f({x_1})} \over {{x_2} – {x_1}}} = {x_1} + {x_2} – 6 > 0\) (vì x1 > 3; x2 > 3)
Vậy hàm số y = x2 – 6x + 5 đồng biến trên \((3;+∞)\)
Bảng biến thiên
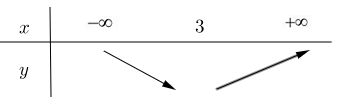
c)
Với mọi x1, x2 ∈ \((-∞; +∞)\) , ta có x1 < x2
\(\Rightarrow\) x12005 < x22005
\(\Rightarrow\) x12005 + 1 < x22005 + 1
hay f(x1) < f(x2) (y = f(x) = x2005 + 1).
Từ đấy ta có, hàm số đã cho đồng biến trên \((-∞; +∞)\)

