Đề toán tổng hợp cuối năm Sách bài tập Toán Hình học 10. Giải bài 16, 17, 18 trang 198, 199 Sách bài tập Toán Hình học 10. Câu 16: Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật có một đỉnh là O…
Bài 16: Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật có một đỉnh là O, diện tích bằng 12 và đường tròn ngoại tiếp (T) của có có phương trình là \({\left( {x – {5 \over 2}} \right)^2} + {y^2} = {{25} \over 4}\). Tìm tọa độ các đỉnh còn lại của hình chữ nhật.

(Xem hình 3.39)
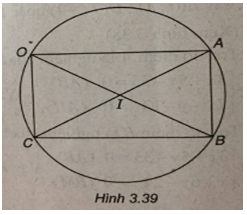
Đường tròn (T) có tâm \(I\left( {{5 \over 2};0} \right)\) và bán kính \(R = {5 \over 2}\).
\(\overrightarrow {OB} = 2\overrightarrow {OI} = \left( {5;0} \right)\) suy ra B(5 ; 0). Đặt A(x ; y) ta có hệ phương trình:
\(\eqalign{
& \left\{ \matrix{
{\left( {x – {5 \over 2}} \right)^2} + {y^2} = {{25} \over 4} \hfill \cr
\sqrt {{x^2} + {y^2}} .\sqrt {{{\left( {5 – x} \right)}^2} + {y^2}} = 12 \hfill \cr} \right. \cr
& \Leftrightarrow \left\{ \matrix{
{y^2} = {{25} \over 4} – {\left( {x – {5 \over 2}} \right)^2} \hfill \cr
\left[ {{x^2} + 5x – {x^2}} \right]\left[ {{{\left( {5 – x} \right)}^2} + 5x – {x^2}} \right] = 144 \hfill \cr} \right. \cr} \)
\( \Leftrightarrow \left\{ \matrix{
{y^2} = 5x – {x^2} \hfill \cr
\left[ \matrix{
x = {9 \over 5} \hfill \cr
y = {{16} \over 5} \hfill \cr} \right. \hfill \cr} \right.\)
Vậy ta được
\(A\left( {{9 \over 5};{{12} \over 5}} \right)\), \(C\left( {{6 \over 5};{{ – 12} \over 5}} \right)\)
Hoặc \(A\left( {{9 \over 5};{{ – 12} \over 5}} \right)\), \(C\left( {{6 \over 5};{{12} \over 5}} \right)\)
Bài 17: Trong mặt phẳng tọa độ Oxy, cho hai đường tròn:
(C1) : \({\left( {x – 2} \right)^2} + {\left( {y – 2} \right)^2} = 4\)
và (C2) : \({\left( {x – 5} \right)^2} + {\left( {y – 3} \right)^2} = 16\)
Advertisements (Quảng cáo)
a) Chứng minh rằng hai đường tròn (C1) , (C2) cắt nhau ;
b) Tìm tọa độ giao điểm của hai tiếp tuyến chung của (C1) và (C2).

(Xem hình 3.40)
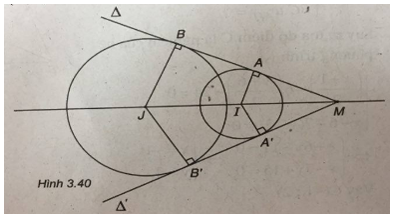
a) (C1) có tâm I(2 ; 2) và bán kính \({R_1} = 2\)
(C2) có tâm J(5 ; 3) và bán kính \({R_2} = 4\)
Ta có:
Advertisements (Quảng cáo)
\(IJ = \sqrt {{{\left( {5 – 2} \right)}^2} + {{\left( {3 – 2} \right)}^2}} = \sqrt {10} .\)
Do: \({R_2} – {R_1} < IJ < {R_2} + {R_1}\)
Nên (C1) và (C2) cắt nhau tại hai điểm phân biệt.
b) Gọi \(\Delta \) và \(\Delta’ \) là hai tiếp tuyến chung của (C1) và (C2) . \(\Delta \) tiếp xúc với (C1) và (C2) lần lượt tại A, B. \(\Delta’ \) tiếp xúc với (C1) và (C2) lần lượt tại A’, B’.
Ta có:
\(\left\{ \matrix{
d(I,\Delta ) = d(I,{\Delta’}) = {R_1} = 2 \hfill \cr
d(J,\Delta ) = d(J,{\Delta’}) = {R_2} = 4 \hfill \cr} \right. \Rightarrow IJ,\Delta \) và \(\Delta’ \) đồng quy tại M.
\(\eqalign{
& {{JM} \over {IM}} = {{JB} \over {IA}} = {{{R_2}} \over {{R_1}}} = 2 \cr
& \Rightarrow \overrightarrow {JM} = 2\overrightarrow {JI} \cr
& \Rightarrow \left\{ \matrix{
{x_M} – 5 = 2.\left( {2 – 5} \right) \hfill \cr
{y_M} – 3 = 2.(2 – 3 \hfill \cr} \right. \cr
& \Rightarrow \left\{ \matrix{
{x_M} = – 1 \hfill \cr
{y_M} = 1. \hfill \cr} \right. \cr} \)
Vậy ta được M(-1 ; 1).
Bài 18: Trong mặt phẳng tọa độ Oxy, cho elip (E): \({{{x^2}} \over 4} + {y^2} = 1\) và điểm \(A\left( { – 1;{1 \over 2}} \right)\). Gọi d là đưởng thẳng đi qua A có hệ số góc là m. Xác định m để d cắt (E) tại hai điểm phân biệt M và N sao cho A là trung điểm của MN.

(Xem hình 3.41)
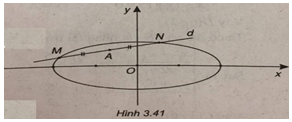
Phương trình đường thẳng d có dạng
\(y – {1 \over 2} = m(x + 1)\)
\( \Leftrightarrow y = m(x + 1) + {1 \over 2}.\)
Phương trình hoành độ giao điểm của d và (E) là :
\(\eqalign{
& {{{x^2}} \over 4} + {\left( {mx + m + {1 \over 2}} \right)^2} = 1 \cr
& \Leftrightarrow {x^2} + 4{\left[ {mx + \left( {m + {1 \over 2}} \right)} \right]^2} = 4 \cr} \)
\(\Leftrightarrow \left( {4{m^2} + 1} \right){x^2} + 4\left[ {\left( {2m + 1} \right)m} \right]x + 4{\left( {m + {1 \over 2}} \right)^2} – 4 = 0.\)
A là trung điểm của MN
\(\eqalign{
& \Leftrightarrow {{{x_M} + {x_N}} \over 2} = {x_A} \cr
& \Leftrightarrow {{ – 4(2{m^2} + m)} \over {2(4{m^2} + 1)}} = – 1 \cr} \)
\( \Leftrightarrow 4{m^2} + 2m = 4{m^2} + 1 \Leftrightarrow m = {1 \over 2}.\)

