Bài 7: Vẽ đồ thị của các hàm số sau và xét tính chẵn lẻ của chúng
a) \(y = – {2 \over 3}x + 2\)
b) \(y = {4 \over 3}x – 1\)
c) \(y = 3x\)
d) y = 5
e) \(y = \sqrt 2 – 1\)

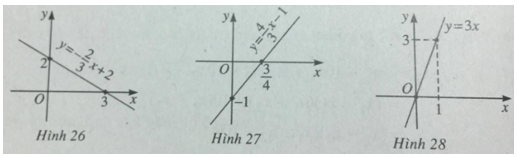
a) Đồ thị là hình 26. Hàm số không là hàm số chẵn, không là hàm số lẻ.
b) Đồ thị là hình 27. Hàm số không là hàm số chẵn, không là hàm số lẻ.
Advertisements (Quảng cáo)
c) Đồ thị là hình 28. Hàm số là hàm số lẻ.
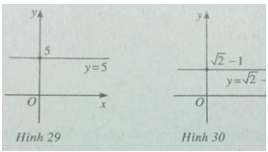
d) Đồ thị là hình 29. Hàm số là hàm số chẵn.
e) Đồ thị là hình 30. Hàm số là hàm số chẵn.
Bài 8; Vẽ đồ thị hàm số
Advertisements (Quảng cáo)
\(y = \left\{ \matrix{
2x – 1,x \ge – 1 \hfill \cr
{1 \over 2}x + 1,x < 1 \hfill \cr} \right.\)

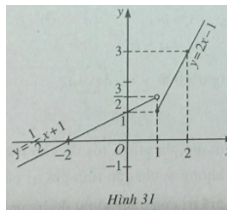
Đồ thị hàm số được vẽ trên hình 31. Điểm (1 ;1) thuộc đồ thị, điểm \((1;{3 \over 2})\) không thuộc đồ thị.
Bài 9: Viết phương trình đường thẳng song song với đường thẳng y = 3x – 2 và đi qua điểm
a) M (2 ;3) ;
b) N (-1 ;2).

Các đường thẳng đều có phương trình dạng y = ax+b . Các đường thẳng song song với nhau đều có cùng một hệ số a. Do đó các phương trình của các đường thẳng song song với đường thẳng y = 3x – 2 đều có hệ số a = 3
a)Phương tình cần tìm có dạng y = 3x + b .
Vì đường thẳng đi qua điểm M(2;3), nên ta có \(3 = 3.2 + b \Leftrightarrow b = – 3\)
Vậy phương trình của đường thẳng đó là y = 3x – 3
b) y = 3x + 5

