Câu 1: Trong các mệnh đề sau, mệnh đề nào đúng?
a) Hai đường thẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song
b) Hai mặt phẳng phân biệt cùng vuông góc với một đường thẳng thì chúng song song
c) Mặt phẳng \((α)\) vuông góc với đường thẳng \(b\) mà \(b\) vuông góc với đường thẳng \(a\), thì \(a\) song song với \((α)\)
d) Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì chúng song song.
e) Hai đường thẳng cùng vuông góc với một đường thẳng thì chúng song song.
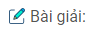
Câu a đúng
\(\left\{ \matrix{
a \bot (P) \hfill \cr
b \bot (P) \hfill \cr} \right. \Rightarrow a//b\)
Câu b đúng
\(\left\{ \matrix{
(P) \bot a \hfill \cr
(Q) \bot a \hfill \cr} \right. \Rightarrow (P)//(Q)\)
Câu c) sai: Vì \(a\) có thể thuộc mp \((α)\)
Câu d) sai: Hai mp \((α)\) và \((β)\) cùng vuông góc với mp \((P)\) thì \((α)\) và \((β)\) vẫn có thể cắt nhau và trong trường hợp này thì giao tuyến của \((α)\) và \((β)\) vuông góc với mp \((P)\).
Câu e) sai: Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì có thể không cùng thuộc một mặt phẳng, khi đó chúng cắt nhau.
Câu 2: Trong các khẳng định sau đây, điều nào đúng?
a) Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại.
b) Qua một điểm có duy nhất một mặt phẳng vuông góc với mặt phẳng cho trước.
c) Qua một đường thẳng có duy nhất một mặt phẳng vuông góc với một mặt phẳng khác cho trước.
d) Đường thẳng nào vuông góc với cả hai đường thẳng chéo nhau cho trước là đường vuông góc chung của hai đường thẳng đó.
Câu a) đúng: Khoảng cách của hai đường thẳng chéo nhau là đoạn ngắn nhất trong các đoạn thẳng nối hai điểm bất kì nằm trên hai đường thẳng ấy và ngược lại (xem mục c) Tính chất của khoảng cách giữa hai đường thẳng chéo nhau)
Câu b) sai: Qua một điểm, ta có thể vẽ được vô số mặt phẳng vuông góc với một mặt phẳng cho trước.
Câu c) sai: Vì trong trường hợp đường thẳng vuông góc với mặt phẳng thì ta có vô số mặt phẳng vuông góc với mặt phẳng cho trước vì bất kì mặt phẳng nào chứa đường thẳng cũng đều vuông góc với mặt phẳng cho trước.
Advertisements (Quảng cáo)
Để có khẳng định đúng, ta phải nói: “Qua một đường thẳng không vuông góc với một mặt phẳng có duy nhất một mặt phẳng vuông góc với mặt phẳng đã cho”.
Câu d) sai: Vì đường vuông góc chung của hai đường thẳng phải cắt cả hai đường thẳng ấy.
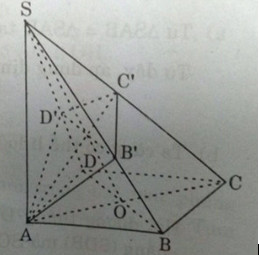
Câu 3: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a\), cạnh \(SA\) bằng \(a\) và vuông góc với mặt phẳng \((ABCD)\).
a) Chứng minh rằng bốn mặt bên của hình chóp là những tam giác vuông.
b) Mặt phẳng \((α)\) đi qua \(A\) và vuông góc với cạnh \(SC\) lần lượt cắt \(SB, SC\) và \(SD\) tại \(B’, C’\) và \(D’\). Chứng minh \(B’D’\) song song với \(BD\) và \(AB’\) vuông góc với \(SB\).
a)
\(SA ⊥(ABCD)\) nên \(AB\) là hình chiếu của \(SB\) trên \(mp(ABCD)\)
\(ABCD\) là hình vuông nên \(BC ⊥AB\). Ta có:
\(\left. \matrix{
SA \bot (ABCD) \hfill \cr
BC \bot AB \hfill \cr} \right\}\)
\(⇒ SB⊥BC\) (theo định lí ba đường vuông góc)
\(⇒ Δ SBC\) là tam giác vuông tại \( B\)
Chứng minh tương tự \(ΔSDA\) vuông tại \(D\)
Advertisements (Quảng cáo)
\(SA ⊥(ABCD) ⇒ SA ⊥ AB ⇒ Δ SAB\) vuông tại \(A\)
\(SA\bot AD\)\( ⇒ Δ SAD\) vuông tại \(A\)
b)
\(\left. \matrix{
SA \bot DB \hfill \cr
AC \bot BD \hfill \cr} \right\} \Rightarrow DB \bot (SAC)\) (1)
Ta lại có:
\(\eqalign{
& \left. \matrix{
BC \bot SB \hfill \cr
BC \bot AB \hfill \cr} \right\} \Rightarrow BC \bot (SAB);AB’ \subset (SAB)(2) \cr
& \Rightarrow AB’ \bot BC \cr
& \left. \matrix{
AB’ \subset (\alpha ) \hfill \cr
SC \bot (\alpha ) \hfill \cr} \right\} \Rightarrow AB’ \bot SC(3) \cr} \)
Chứng minh tương tự ta có: \(AD’⊥SC\)
Hai tam giác vuông \(SAB\) và \(SAD\) bằng nhau mà \(AB’\) và \(AD’\) là các đường cao tương ứng nên \(AD’= AB’\) (4)
Ta cũng có: \(SB’=SD’\);
\(ΔBSC = Δ DSC\) \(⇒ \widehat{ BSC} = \widehat{ CSD}\)
Do đó \(ΔB’SC’ = Δ D’SC’\)
Từ đây suy ra: \(C’D’ = C’B’\) (5)
Từ (4) và (5) suy ra \(A\) và \(C’\) nằm trên đường trung trực của \(D’B’\) do đó \(D’B’⊥ AC’\) (6)
Mặt khác: \(SC⊥(α)\); \(D’B’⊂ (α)\) \( ⇒ SC⊥D’B’\) (7)
Từ (6) và (7) suy ra: \(D’B’⊥(SAC)\) (8)
Từ (1) và (8) ta thấy rằng \(DB\) và \(D’B’\) cùng vuông góc với mặt phẳng \((SAC)\) nên \(D’B’//DB\)
Ta có:
\(\left. \matrix{
AB’ \bot BC \hfill \cr
AB’ \bot SC \hfill \cr} \right\} \Rightarrow AB’ \bot (SBC) \Rightarrow AB’ \bot SB\)
Câu 4: Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi cạnh \(a\) và có góc \(\widehat{ BAD} = 60^0\). Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Đường thẳng SO vuông góc với mặt phẳng (ABCD) và \(SO = {{3a} \over 4}\) . Gọi \(E\) là trung điểm của đoạn \(BC\) và \(F\) là trung điểm của đoạn \(BE\).
a) Chứng minh mặt phẳng \( (SOF)\) vuông góc với mặt phẳng \((SBC)\)
b) Tính các khoảng cách từ \(O\) và \(A\) đến mặt phẳng \((SBC)\)
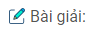
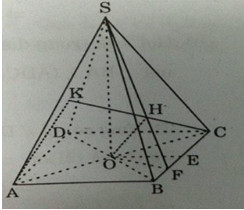
a) Theo giả thiết \(\widehat{ BAD} = 60^0\) nên theo tính chất của hình thoi \(\widehat{ BCD} = 60^0\) hay tam giác \(BDC\) đều.
Xét tam giác \(BOE\) có \(BO=BE={a\over 2}\) và \(\widehat{ OBE} = 60^0\) nên tam giác \(BOE\) đều
Do đó \(OF\) là đường cao và ta được \(OF ⊥BC\).
\(\left. \matrix{
SO \bot (ABCD) \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow SF \bot BC\)
(Định lí 3 đường vuông góc)
\(\left. \matrix{
SF \bot BC \hfill \cr
{\rm{OF}} \bot {\rm{BC}} \hfill \cr} \right\} \Rightarrow BC \bot (SOF)\)
Mà \(BC ⊂ (SBC)\)
Suy ra \((SOF) ⊥ (SBC)\)
b) Vì \((SOF) ⊥ (SBC)\) và hai mặt phẳng này giao nhau theo giao tuyến \(SF\) nên nếu từ điểm \(O\) ta kẻ \(OH⊥SF\) thì \(OH⊥(SBC)\) và \(OH\) chính là khoảng cách từ \(O\) đến \((SBC)\)
Ta có:
\(\eqalign{
& SO = {{3a} \over 4}{\rm{;OF = }}{{a\sqrt 3 } \over 4} \Rightarrow SF = {{a\sqrt 3 } \over 2} \cr
& OH.SF = SO.{\rm{OF}} \Rightarrow {\rm{OH = }}{{3a} \over 8} \cr} \)
Gọi \(K\) là hình chiếu của \(A\) trên \((SBC)\), ta có \(AK//OH\)
Trong \(ΔAKC\) thì \(OH\) là đường trung bình, do đó:
\(AK = 2OH \Rightarrow AK = {{3a} \over 4}\)

