Câu 1: Trong các mệnh đề sau đây, mệnh đề nào là đúng?
(A) Từ \(\overrightarrow {AB} = 3\overrightarrow {AC} \) ta suy ra \(\overrightarrow {BA} = – 3\overrightarrow {CA} \)
(B) Từ \(\overrightarrow {AB} = – 3\overrightarrow {AC} \) ta suy ra \(\overrightarrow {CB} = 2\overrightarrow {AC} \)
(C) Vì \(\overrightarrow {AB} = – 2\overrightarrow {AC} + 5\overrightarrow {AD} \) nên bốn điểm \(A, B, C\) và \(D\) cùng thuộc một mặt phẳng
(D) Nếu \(\overrightarrow {AB} = – {1 \over 2}\overrightarrow {BC} \) thì \(B\) là trung điểm của đoạn \(AC\)
a) Vì
\(\left\{ \matrix{
\overrightarrow {AB} = – \overrightarrow {BA} \hfill \cr
\overrightarrow {AC} = – \overrightarrow {CA} \hfill \cr} \right.\)
nên từ:
\(\overrightarrow {AB} = 3\overrightarrow {AC} \) ta suy ra \(\overrightarrow {BA} = 3\overrightarrow {CA} \)
Vậy a) là sai
b) Ta có:
\(\overrightarrow {AB} = – 3\overrightarrow {AC} \Rightarrow \overrightarrow {AC} + \overrightarrow {CB} = – 4\overrightarrow {AC} \Rightarrow \overrightarrow {CB} = – 4\overrightarrow {AC} \)
Vậy b) sai
Advertisements (Quảng cáo)
c) \(\overrightarrow {AB} = – 2\overrightarrow {AC} + 5\overrightarrow {AD} \): Đẳng thức nàu chứng tỏ ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng, tức là 4 điểm \(A, B, C, D\) cùng nằm trong một mặt phẳng.
Vậy c) đúng
d) \(\overrightarrow {AB} = – {1 \over 2}\overrightarrow {BC} \Rightarrow \overrightarrow {BA} = {1 \over 2}BC\)
Điều này chứng tỏ hai vecto \(\overrightarrow {BA} ,\overrightarrow {BC} \) cùng phương, do đó điểm B nằm ngoài đoạn thẳng \(AC\), \(B\) không là trung điểm của \(AC\)
Vậy d) sai
Kết quả: trong bốn mệnh đề trên, chỉ có c) đúng.
Câu 2: Tìm mệnh đề sai trong các mệnh đề sau đây:
A. Vì \(\overrightarrow {NM} + \overrightarrow {NP} = \overrightarrow 0 \) nên \(N\) là trung điểm của đoạn \(MP\)
B. Vì \(I\) là trung điểm của đoạn \(AB\) nên từ một điểm \(O\) bất kì ta có: \(\overrightarrow {OI} = {1 \over 2}(\overrightarrow {OA} + \overrightarrow {ON} )\)
Advertisements (Quảng cáo)
C. Từ hệ thức \(\overrightarrow {AB} = 2\overrightarrow {AC} – 8\overrightarrow {AD} \) ta suy ra ba vecto \(\overrightarrow {AB} ,\overrightarrow {AC} ,\overrightarrow {AD} \) đồng phẳng
D. Vì \(\overrightarrow {AB} + \overrightarrow {BC} + \overrightarrow {CD} + \overrightarrow {DA} = 0\) nên bốn điểm \(A, B, C, D\) cùng thuộc một mặt phẳng.
(A) Mệnh đề A đúng vì \(N\) là trung điểm của đoạn \(MP\) là:
\(\overrightarrow {NM} = – \overrightarrow {NP} \Rightarrow \overrightarrow {NM} + \overrightarrow {NP} = 0\)
(B) Mệnh đề B đúng
\(\eqalign{
& \overrightarrow {OI} = \overrightarrow {OA} + \overrightarrow {AI} \cr
& \overrightarrow {OI} = \overrightarrow {OB} + \overrightarrow {BI} \Rightarrow 2\overrightarrow {OI} = \overrightarrow {OA} + \overrightarrow {OB} + (\overrightarrow {AI} + \overrightarrow {BI} ) \cr} \)
\(I\) là trung điểm của đoạn thẳng \(AB\) thì:
\(\overrightarrow {AI} + \overrightarrow {BI} = \overrightarrow 0 \Rightarrow 2\overrightarrow {OI} = \overrightarrow {OA} + \overrightarrow {OB} \)
(C) Mệnh đề C đúng (xem định lí 1 – bài 1- chương 3)
(D) Mệnh đề D là sai
Vậy chọn D
Câu 3: Trong các mệnh đề sau, kết quả nào đúng?
Cho hình lập phương \(ABCD.EFGH\) có cạnh bằng \(a\) và \(O\) là trung điểm của \(AG\), ta có \(\overrightarrow {AB} .\overrightarrow {EG} \) bằng :
A. \(a^2\) B. \( a^2\sqrt 2\)
C. \(a^2\sqrt3\) D. \({{{a^2}\sqrt 2 } \over 2}\)
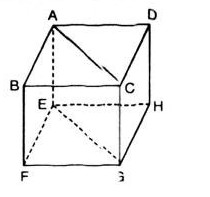
Ta có:
\(\eqalign{
& \overrightarrow {AB} .\overrightarrow {EG} = \overrightarrow {EF} .\overrightarrow {EG} \cr
& \Rightarrow \overrightarrow {AB} .\overrightarrow {EG} = |\overrightarrow {AB} |.|\overrightarrow {EG} |.cos{45^0} \cr
& \Rightarrow \overrightarrow {AB} .\overrightarrow {EG} = a.a\sqrt 2 .{{\sqrt 2 } \over 2} = {a^2} \cr} \)
Vậy A đúng.

