Bài 5: Cho hình lập phương \(ABCD.A’B’C’D’\) cạnh \(a\).
a) Chứng minh rằng \(B’D\) vuông góc với mặt phẳng \((BA’C’)\).
b) Tính khoảng cách giữa hai mặt phẳng \((BA’C’)\) và \((ACD’)\).
c) Tính khoảng cách giữa hai đường thẳng \(BC’\) và \(CD’\).
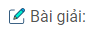
(H.3.66)
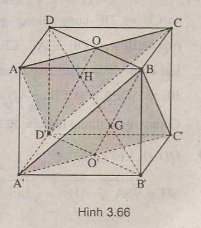
a) Có \(B’A’ = B’B = B’C’ \Rightarrow B’\) thuộc trục của tam giác \(A’BC’\). (1)
\(DA’ = DB = DC’\) (đường chéo các hình vuông bằng nhau) \(\Rightarrow D\) cũng thuộc trục của tam giác \(A’BC’ \) (2)
Từ (1) và (2) \(\Rightarrow B’D\) vuông góc với \((BA’C’)\).
b) Chứng minh tương tự ta được \(B’D\bot (ACD’)\)
Hai mặt phẳng \((BA’C’)\) và \((ACD’)\) cùng vuông góc với \(B’D\) (tại \(G\) và \(H\)) nên chúng song song với nhau và khoảng cách giữa chúng bằng \(GH\).
Ta có:
\(O’G//D’H\), \(O’\) là trung điểm của \(B’D’\) nên theo định lí Ta lét thì \(G\) là trung điểm của \(B’H\) hay \(GB’=GH\) (3)
\(OH//GB\), \(O\) là trung điểm của \(BD\) nên theo định lí Ta lét thì \(H\) là trung điểm của \(DG\) hay \(HG=HD\) (4)
Từ (3) và (4) suy ra: \(GH=\frac{B’D}{3}=\frac{a\sqrt{3}}{3}\)
c) \(BC’ ⊂ (BA’C’)\); \(CD’ ⊂ (ACD’)\), mà hai mặt phẳng này song song
Do đó, \(d(BC’, CD’) = d((BA’C’),(ACD’))= \frac{a\sqrt{3}}{3}.\)
(Khoảng cách giữa hai đường thẳng chéo nhau bằng khoảng cách giữa hai mặt phẳng song song lần lượt chứa hai đường thẳng đó).
Bài 6: Chứng minh rằng nếu đường thẳng nối trung điểm hai cạnh \(AB\) và \(CD\) của tứ diện \(ABCD\) là đường vuông góc chung của \(AB\) và \(CD\) thì \(AC = BD\) và \(AD = BC\).
Advertisements (Quảng cáo)
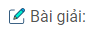
(H.3.67)
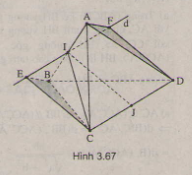
Qua \(I\) kẻ đường thẳng \(d // CD\), lấy trên \(d\) điểm \(E, F\) sao cho \(IE = IF = \frac{CD}{2}\) (\(I\) là trung điểm của \(EF\)). \(IJ\) vuông góc với \(CD\) \(\Rightarrow IJ\) vuông góc với \(EF\), mà \(IJ\) cũng vuông góc với \(AB\Rightarrow IJ \bot (AEBF)\).
Ta có \(CDFE\) là hình bình hành có \(IJ\) là đường trung bình
Do đó \(CE\) và \(DF\) cùng song song với \(IJ\)
Suy ra \(CE\) và \(DF\) cùng vuông góc với mp \((AEBF)\)
\(\Rightarrow DF ⊥ AF, CE ⊥ IE\).
\(\Delta AIF = \Delta BIE(c.g.c)\) suy ra: \(AF=BE\)
Xét \(∆DFA\) và \(∆CEB\) có:
+) \(\widehat E = \widehat F( = {90^0})\)
+) \(AF=BE\)
Advertisements (Quảng cáo)
+) \(DF=CE\)
\(\Rightarrow ∆DFA=∆CEB(c.g.c)\)
\(\Rightarrow AD = BC\).
Chứng minh tương tự ta được \(BD = AC\).
Bài 7: Cho hình chóp tam giác đều \(S.ABC\) có cạnh đáy bằng \(3a\), cạnh bên bằng \(2a\). Tính khoảng cách từ \(S\) tới mặt đáy \((ABC)\).
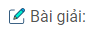
(H.3.68)
Gọi \(H\) là trực tâm tam giác \(ABC\).
\(d(S,(ABC))=SH\)
Gọi \(N\) là trung điểm của \(BC\).
Tam giác \(ABC\) đều nên \(AN={{3a\sqrt 3 } \over 2}\)
\(AH={2 \over 3}AN = a\sqrt 3 \)
Áp dung định lí Pytago vào tam giác vuông \(SAH\) ta có:
\(S{A^2} = S{H^2} + A{H^2}\)
\(SH = \sqrt{SA^{2}-AH^{2}}=\sqrt{4a^{2}-(a\sqrt{3})^{2}}=a.\)
Vậy khoảng cách từ \(S\) đến mặt phẳng \((ABC)\) bằng \(a\).
Bài 8: Cho tứ diện đều \(ABCD\) cạnh \(a\). Tính khoảng cách giữa hai cạnh đối diện của tứ diện.
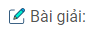
(H.3.69)
Gọi \(M, N\) lần lượt là trung điểm của \(AD\) và \(BC\),
\(\Delta BAC = \Delta BDC(c.c.c)\) \( \Rightarrow AN = DN\) (hai đường trung tuyến tương ứng của hai tam giác bằng nhau)
Tam giác \(AND\) cân tại \(N\), nên \(MN\) vừa là đường trung tuyến đồng thời là đường cao do đó \(MN\bot AD\) (1)
Chứng minh tương tự ta được: \(MN\bot BC\) (2)
Từ (1) và (2) suy ra \(MN\) là đường vuông góc chung của \(BC\) và \(AD\)
Tam giác \(ABC\) đều nên \(AN={{a\sqrt 3 } \over 2}\)
Áp dụng định lí Pytago vào tam giác vuông \(AMN\) ta có:
\(A{N^2} = M{N^2} + A{M^2}\)
\(MN = \sqrt {A{N^2} – A{M^2}} = \sqrt {{{3{a^2}} \over 4} – {{{a^2}} \over 4}} = {{a\sqrt 2 } \over 2}\)

