Bài 1: Trong các mệnh đề sau đây, mệnh đề nào đúng?
a) Đường thẳng \(∆\) là đường thẳng vuông góc chung của hai đường thẳng \(a\) và \(b\) nếu \(∆\) vuông góc với \(a\) và \(∆\) vuông góc với \(b\);
b) Gọi \((P)\) là mặt phẳng song song với cả hai đường thẳng \(a, b\) chéo nhau. Khi đó đường vuông góc chung \(∆\) của \(a\) và \(b\) luôn luôn vuông góc với \((P)\);
c) Gọi \(∆\) là đường vuông góc chung của hai đường thẳng chéo nhau \(a\) và \(b\) thì \(∆\) là giao tuyến của hai mặt phẳng \((a, ∆)\) và \((b, ∆)\);
d) Cho hai đường thẳng chéo nhau \(a\) và \(b\). Đường thẳng nào đi qua một điểm \(M\) trên \(a\) đồng thời cắt \(b\) tại \(N\) và vuông góc với \(b\) thì đó là đường vuông góc chung của \(a\) và \(b\);
e) Đường vuông góc chung \(∆\) của hai đường thẳng chéo nhau \(a\) và \(b\) nằm trong mặt phẳng chứa đường này và vuông góc với đường kia.
a) Sai;
b)Đúng;
c) Đúng;
d) Sai;
e) Sai.
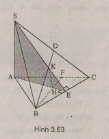
Bài 2: Cho tứ diện \(S.ABC\) có \(SA\) vuông góc với mặt phẳng \((ABC)\). Gọi \(H, K\) lần lượt là trực tâm của tam giác \(ABC\) và \(SBC\).
a) Chứng minh ba đường thẳng \(AH, SK, BC\) đồng quy.
b) Chứng minh rằng \(SC\) vuông góc với mặt phẳng \((BHK)\) và \(HK\) vuông góc với mặt phẳng \((SBC)\).
c) Xác định đường vuông góc chung của \(BC\) và \(SA\).
Advertisements (Quảng cáo)
a) Trong \((ABC)\), gọi \(E = AH ∩ BC\).
\(H\) là trực tâm của tam giác \(ABC\) nên \(AE\bot BC\) (1)
\(SA\bot (ABC)\Rightarrow SA\bot BC\) (2)
Từ (1) và (2) suy ra \(BC ⊥ (SAE)\)\( \Rightarrow BC ⊥ SE\).
\(K\) là trực tâm của tam giác \(SBC\Rightarrow SE \) đi qua \(K\) \(\Rightarrow AH, BC, SK\) đồng quy tại \(E\).
b) Trong \((ABC)\) gọi \(F = BH ∩ AC\), trong \((SBC)\) gọi \(D = BK ∩ SC\). Khi đó \((BHK) \equiv (BDF)\)
\(K\) là trực tâm của tam giác \(SBC\) nên \(BD\bot SC\) (*)
\(H\) là trực tâm của tam giác \(ABC\) nên \(BF\bot AC\) (3)
\(SA\bot (ABC)\Rightarrow SA\bot BF\) (4)
Từ (3) và (4) suy ra \(BF\bot (SAC)\Rightarrow BF\bot SC\) (2*)
Advertisements (Quảng cáo)
Từ (*) và (2*) suy ra \(SC\bot (BDF) \equiv (BHK)\).
c) \(AE\bot BC\) và \(SA\bot AE\Rightarrow AE\) là đường vuông góc chung của \(BC\) và \(SA\).
Bài 3: Cho hình lập phương \(ABCD.A’B’C’D’\) cạnh \(a\). Chứng minh rằng các khoảng cách từ các điểm \(B, C, D, A’, B’, D’\) đến đường chéo \(AC’\) đều bằng nhau. Tính khoảng cách đó.
(H.3.64)
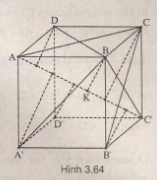
Gọi \(K\) là hình chiếu của \(B\) trên \(AC’\).
Xét tam giác \(ABC’\) vuông tại \(B\), ta có:
\(\frac{1}{BK^{2}}=\frac{1}{BA^{2}}+\frac{1}{BC^{2}}=\frac{1}{a^{2}}+\frac{1}{(a\sqrt{2})^{2}}=\frac{3}{2a^{2}}\)
\(\Rightarrow BK=\frac{a\sqrt{6}}{3}.\)
Ta có:
\(\Delta ABC’ = \Delta C’CA = \Delta ADC’ = \Delta AA’C’ = \Delta C’B’A = \Delta C’D’A(c.g.c)\)
Do đó khoảng cách từ \(B, C, D, A’, B’, D’\) tới \(AC’\) đều bằng \( \frac{a\sqrt{6}}{3}\) vì chúng đều là chiều cao của các tam giác vuông bằng nhau.
Bài 4: Cho hình hộp chữ nhật \(ABCD.A’B’C’D’\) có \(AB = a, BC= b, CC’ = c\).
a) Tính khoảng cách từ \(B\) đến mặt phẳng \((ACC’A’)\).
b) Tính khoảng cách giữa hai đường thẳng \(BB’\) và \(AC’\).
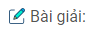
(H.3.65)
a) Trong \((ABCD)\) kẻ \(BH\) vuông góc với \(AC\) (1)
\(CC’\bot (ABCD)\Rightarrow CC’\bot BH\) (2)
Từ (1) và (2) suy ra \(BH\bot (ACC’A’)\).
\(BH\) là đường cao trong tam giác vuông \(ABC\) nên ta có:
\({1 \over {B{H^2}}} = {1 \over {A{B^2}}} + {1 \over {B{C^2}}}\)
\(\Rightarrow BH=\frac{ab}{\sqrt{a^{2}+b^{2}}}.\)
b) \(AC’\subset (ACC’A’)\), mà \(BB’ // (ACC’A’)\) \(\Rightarrow d(BB’, AC’) = d(B,(ACC’A’))=BH=\frac{ab}{\sqrt{a^{2}+b^{2}}}.\)
(Chú ý: Khoảng cách giữa hai đường thẳng chéo nhau \(a\) và \(b\) bằng khoảng cách giữa \(a\) và \(mp (P)\) chứa \(b\) đồng thời song song với \(a\)).

