Bài 9: Cho hình chóp tam giác đều \(S.ABC \) có \(SH\) là đường cao. Chứng minh \(SA ⊥ BC\) và \(SB ⊥ AC\).
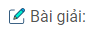
Chóp tam giác đều nên ta có \(H\) là trực tâm của tam giác \(ABC\)
\(SH ⊥ (ABC) \Rightarrow SH ⊥ BC\) và \(AH ⊥ BC\) (vì \(H\) là trực tâm)
Suy ra \( BC ⊥ (SAH)\)
\(SA\subset (SAH)\Rightarrow BC ⊥ SA\).
Chứng minh tương tự, ta có \(SB ⊥ AC\).
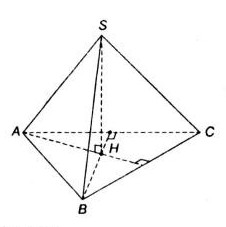
Bài 10: Cho hình chóp tứ giác đều \(S.ABCD\) có các cạnh bên và cạnh đáy đều bằng \(a\). Gọi \(O\) là tâm của hình vuông \( ABCD\).
a) Tính độ dài đoạn thẳng \(SO\).
b) Gọi \(M\) là trung điểm của đoạn \(SC\). Chứng minh hai mặt phẳng \((MBD)\) và \((SAC)\) vuông góc với nhau.
c) Tính độ dài đoạn \(OM\) và tính góc giữa hai mặt phẳng \((MBD)\) và \((ABCD)\).
Advertisements (Quảng cáo)
a) Hình chóp tứ giác đều nên \(SO\bot (ABCD)\). Do đó \(SO\bot AC\)
Xét tam giác \(SOA\) vuông tại \(O\):
\(SO = \sqrt{SA^{2}-AO^{2}}=\frac{a\sqrt{2}}{2}.\)
b) \(BD\bot AC\) , \(BD\bot SO\) nên \(BD \bot (SAC)\),
Mà \(BD ⊂ (MBD)\) do đó \((MBD) ⊥ (SAC)\).
c) \(OM =\frac{SC}{2}=\frac{a}{2}\) (trung tuyến ứng với cạnh huyền của tam giác vuông thì bằng nửa cạnh ấy).
\( \Delta SDC = \Delta SBC(c.c.c)\) suy ra \(DM=BM\) suy ra tam giác \(BDM\) cân tại \(M\)
Advertisements (Quảng cáo)
\(OM\) vừa là trung tuyến đồng thời là đường cao nên \(OM\bot BD\)
\(\left. \matrix{
(MBD) \cap (ABCD) = BD \hfill \cr
OM \bot BD \hfill \cr
OC \bot BD \hfill \cr} \right\} \Rightarrow \) góc giữa hai mặt phẳng \((MBD)\) và \((ABCD)\) là \(\widehat {MOC}\)
Ta có \(OM=\frac{SC}{2}=\frac{a}{2}\) hay \(OM=MC\) Tam giác \(OMC\) vuông cân tại \(M\)
\((\widehat{(MBD);(ABCD)})=(\widehat{MOC})=45^{0}.\)
Bài 11: Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là một hình thoi tâm \(I\) cạnh \(a\) và có góc \(A\) bằng \(60^{0},\) cạnh \(SC=\frac{a\sqrt{6}}{2}\) và \(SC\) vuông góc với mặt phẳng \((ABCD)\).
a) Chứng minh mặt phẳng \((SBD)\) vuông góc với mặt phẳng \((SAC)\).
b) Trong tam giác \(SCA\) kẻ \(IK\) vuông góc với mặt phẳng \((SAC)\). Hãy tính độ dài \(IK\)
c) Chứng minh \(\widehat{BKD}=90^{0}\) và từ đó suy ra mặt phẳng \((SAB)\) vuông góc với mặt phẳng \((SAD)\).
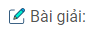
(H.3.50)
a) \(SC\) vuông góc với mặt phẳng \((ABCD)\) suy ra \(SC\bot BD\) (1)
\(ABCD\) là hình thoi nên \(AC\bot BD\) (2)
Từ (1) và (2) suy ra \(BD ⊥ (SAC)\)
\(BD\subset (SBD)\Rightarrow (SBD) ⊥ (SAC)\).
b) Xét tam giác vuông \(ABI\) có: \(AI=AB.\cos 30^0={{a\sqrt 3 } \over 2}\Rightarrow AC = 2AI = a\sqrt 3 \)
Xét tam giác vuông \(SAC\) có: \(SA=\sqrt {A{C^2} + S{C^2}} = \sqrt {3{a^2} + {{6{a^2}} \over 4}} =\frac{3a}{\sqrt{2}}.\)
Hai tam giác vuông \(SCA\) và \(IKA\) đồng dạng (g.g) nên \(\frac{IK}{SC}=\frac{AI}{AS}\Rightarrow IK=\frac{AI.SC}{AS}=\frac{a}{2}.\)
c) \(IK = IB = ID = \frac{a}{2}\) nên tam giác \(BKD\) vuông tại \(K\). Vậy \(\widehat{BKD}=90^{0}.\)
\(SA\) cùng vuông góc với \(BD\) và \(IK\) nên \(SA ⊥ (DKB)\); \(DK\) và \(BK\) cùng vuông góc với \(SA\). Vậy góc \(\widehat {BKD}\) là góc giữa \((SAD)\) và \((SAB)\) và \(\widehat{BKD}=90^{0}\) \(\Rightarrow (SAD) ⊥ (SAB)\).

