Câu 12: Minh họa hình học tập nghiệm của mỗi hệ phương trình sau
\(a)\left\{ {\matrix{
{2x + 3y = 7} \cr
{x – y = 6} \cr} } \right.\)
\(b) \left\{ {\matrix{
{3x + 2y = 13} \cr
{2x – y = – 3} \cr} } \right.\)
\(c) \left\{ {\matrix{
{x + y = 1} \cr
{3x + 0y = 12} \cr} } \right.\)
\(d)\left\{ {\matrix{
{x + 2y = 6} \cr
{0x – 5y = 10} \cr} } \right.\)
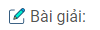
\(a) \left\{ {\matrix{
{2x + 3y = 7} \cr
{x – y = 6} \cr} } \right. \Leftrightarrow \left\{ {\matrix{
{y = – {2 \over 3}x + {7 \over 3}} \cr
{y = x – 6} \cr} } \right.\)
Vẽ đường thẳng \(y = – {2 \over 3}x + {7 \over 3}\)
Cho \(x = 0 \Rightarrow y = {7 \over 3}\) \(\left( {0;{7 \over 3}} \right)\)
Cho \(y = 0 \Rightarrow x = 3,5\) \(\left( {3,5;0} \right)\)
Vẽ đường thẳng y = x – 6
Cho \(x = 0 \Rightarrow y = – 6\) \(\left( {0; – 6} \right)\)
Cho \(y = 0 \Rightarrow x = 6\) \(\left( {6;0} \right)\)
Hai đường thẳng cắt nhau tại A (5; -1)
Nghiệm hệ phương trình: (x ; y) = (5; -1)
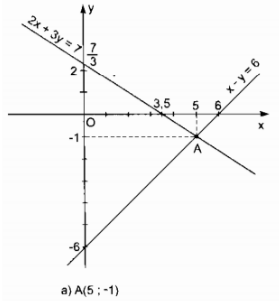
\(b)\left\{ {\matrix{
{3x + 2y = 13} \cr
{2x – y = – 3} \cr} \Leftrightarrow \left\{ {\matrix{
{y = – {3 \over 2}x + {{13} \over 2}} \cr
{y = 2x + 3} \cr} } \right.} \right.\)
Vẽ đường thẳng \(y = – {3 \over 2}x + {{13} \over 2}\)
Cho \(x = 0 \Rightarrow y = 6,5\) (0; 6,5)
Cho \(y = 0 \Rightarrow x = {{13} \over 3}\) \(\left( {{{13} \over 3};0} \right)\)
Vẽ đường thẳng y = 2x + 3
Cho \(x = 0 \Rightarrow y = 3\) (0; 3)
Cho \(y = 0 \Rightarrow x = – 1,5\) (-1,5; 0)
Hai đường thẳng cắt nhau tại B(1; 5)
Vậy nghiệm của hệ phương trình: (x; y) = (1; 5)
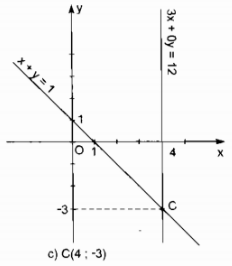
\(c)\left\{ {\matrix{
{x + y = 1} \cr
{3x + 0y = 12} \cr} \Leftrightarrow \left\{ {\matrix{
{y = – x + 1} \cr
{x = 4} \cr} } \right.} \right.\)
Vẽ y = -x + 1
Cho \(x = 0 \Rightarrow y = 1\) (0; 1)
Advertisements (Quảng cáo)
Cho \(y = 0 \Rightarrow x = 1\) (1; 0)
Vẽ x = 4
Hai đường thẳng cắt nhau tại C(4; -3)
Vậy nghiệm của hệ phương trình: (x; y) = (4;- 3)
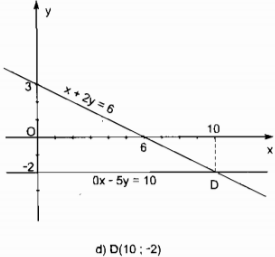
\(d)\left\{ {\matrix{
{x + 2y = 6} \cr
{0x – 5y = 10} \cr} \Leftrightarrow \left\{ {\matrix{
{y = – {1 \over 2}x + 3} \cr
{y = – 2} \cr} } \right.} \right.\)
Vẽ \(y = – {1 \over 2}x + 3\)
Cho \(x = 0 \Rightarrow y = 3\) (0; 3)
Cho \(y = 0 \Rightarrow x = 6\) (6; 0)
Vẽ y = 2
Hai đường thẳng cắt nhau tại D (10; -2)
Vậy nghiệm của hệ phương trình là (x; y) = (10; -2).
Câu 13: Cho hệ phương trình
\(\left\{ {\matrix{
{x + 0y = – 2} \cr
{5x – y = – 9} \cr} } \right.\)
a) Minh họa hình học tập nghiệm của hệ phương trình đã cho. Từ đó xác định nghiệm của hệ.
b) Nghiệm của hệ này có phải là nghiệm của phương trình 3x – 7y = 1 hay không ?
Advertisements (Quảng cáo)
\(a)\left\{ {\matrix{
{x + 0y = – 2} \cr
{5x – y = – 9} \cr} \Leftrightarrow \left\{ {\matrix{
{x = – 2} \cr
{y = 5x + 9} \cr} } \right.} \right.\)
Vẽ x = -2
Vẽ y = 5x + 9
Cho \(x = 0 \Rightarrow y = 9\) (0; 9)
Cho \(y = 0 \Rightarrow x = – {9 \over 5} = – 1,8\) (-1,8; 0)
Đường thẳng x = -2 song song với trục tung
Đường thẳng y = 5x + 9 cắt trục tung nên hai đường thẳng đó cắt nhau tại A(-2; -1). Vậy hệ phương trình có nghiệm: (x; y) = (-2; -1)
b) Thay x = -2; y = -1 vào vế trái của phương trình 3x – 7y = 1 ta có:
\(3\left( { – 2} \right) – 7\left( { – 1} \right) = – 6 + 7 = – 1\)
Vế trái bằng vế phải
Vậy cặp (x; y) = (-2; -1) là nghiệm của phương trình 3x – 7y = 1.
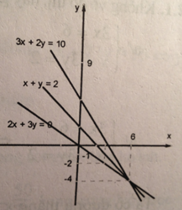
Câu 14: Vẽ hai đường thẳng \(\left( {{d_1}} \right):x + 2y = 2\) và \(\left( {{d_2}} \right):2x + 3y = 0\)
Hỏi đường thẳng \(\left( {{d_3}} \right):3x + 2y = 10\) có đi qua giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) hay không?
Vẽ đường thẳng \({d_1}\) là đồ thị của hàm số \(y = – x + 2\)
Cho \(x = 0 \Rightarrow y = 2\) (0; 2)
Cho \(y = 0 \Rightarrow x = 2\) (2; 0)
Vẽ đường thẳng \({d_2}\) là đồ thị của hàm số \(y = – {2 \over 3}x\)
Đồ thị đi qua O(0; 0)
Cho \(x = 3 \Rightarrow y = – 2\) (3; -2)
Hai đường thẳng có hệ số góc khác nhau chúng cắt nhau tại B(6; -4)
Thay tọa độ của điểm B vào vế trái phương trình đường thẳng \({d_3}\) ta có:
\(3.6 + 2.\left( { – 4} \right) = 18 – 8 = 10\)
Tọa độ của điểm B nghiệm đúng phương trình đường thẳng \({d_3}\)
Vậy đường thẳng \({d_3}:3x + 2y = 10\) đi qua giao điểm của \({d_1}\) và \({d_2}\).
Câu 15: Hỏi bốn đường thẳng sau có đồng quy không
\(\eqalign{
& \left( {{d_1}} \right):3x + 2y = 13 \cr
& \left( {{d_2}} \right):2x + 3y = 7 \cr
& \left( {{d_3}} \right):x – y = 6 \cr
& \left( {{d_4}} \right):5x – 0y = 25 \cr} \)
Vẽ đường thẳng \({d_3}\) là đồ thị của hàm số y = x – 6
Cho \(x = 0 \Rightarrow y = – 6\) (0; -6)
Cho \(y = 0 \Rightarrow x = 6\) (6; 0)
Vẽ đường thẳng \({d_4}\) là đường thẳng x = 5
Đường thẳng x = 5 song song với trục tung
Đường thẳng y = x – 6 cắt trục tung nên hai đường thẳng đó cắt nhau tại điểm C(5; -1)
Nếu \({d_1},{d_2}\) cùng đi qua điểm C(5; -1) thì 4 đường thẳng đó đồng quy
Thay tọa độ của C vào vế trái phương trình đường thẳng \({d_1}\)
\(3.5 + 2.\left( { – 1} \right) = 15 – 2 = 13\)
Tọa độ của điểm C nghiệm đúng phương trình đường thẳng \({d_1}\)
Vậy \({d_1}\) đi qua C (5; -1)
Thay tọa độ của C vào vế trái của phương trình đường thẳng \({d_2}\) ta có:
\(2.5 + 3\left( { – 1} \right) = 10 – 3 = 7\)
Tọa độ của điểm C nghiệm đúng phương trình đường thẳng \({d_2}\). Vậy \({d_2}\) đi qua điểm C (5; -1) nên 4 đường thẳng đó đồng quy tại C (5; -1).