Câu 5: Phải chọn a và b như thế nào để phương trình ax + by = c xác định 1 hàm số bậc nhất của biến x ?
Để phương trình ax + by = c xác định 1 hàm số bậc nhất với biến số x có dạng: \(y = – {a \over b}x + {c \over b}\) thì \(a \ne 0\) và \(b \ne 0\)
Câu 6: Vẽ mỗi cặp đường thẳng sau trong cùng 1 mặt phẳng tọa độ rồi tìm tọa độ giao điểm của 2 đường thẳng đó
a) 2x + y = 1 và 4x – 2y = -10
b) 0,5x + 0,25y = 0,15 và \( – {1 \over 2}x + {1 \over 6}y = – {3 \over 2}\)
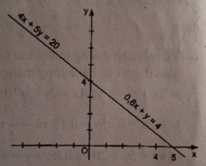
c) 4x + 5y = 20 và 0,8x + y = 4
d) 4x + 5y = 20 và 2x + 2,5y = 5
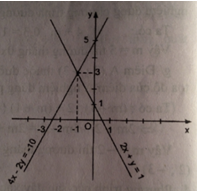
a) Vẽ đường thẳng 2x + y = 1 là đồ thị hàm số y = -2x + 1
Cho \(x = 0 \Rightarrow y = 1\) (0 ; 1)
Cho \(y = 0 \Rightarrow x = {1 \over 2}\) \(\left( {{1 \over 2};0} \right)\)
Vẽ đường thẳng 4x – 2y = -10 là đồ thị hàm số y = 2x + 5
Cho \(x = 0 \Rightarrow y = 5\) (0 ; 5)
Cho \(y = 0 \Rightarrow x = – 2,5\) (-2,5 ; 0)
Hoành độ giao điểm của 2 đường thẳng:
\( – 2x + 1 = 2x + 5 \Leftrightarrow 4x = – 4 \Leftrightarrow x = – 1\)
Tung độ giao điểm: y = -2 (- 1) + 1 = 2 + 1 = 3
Advertisements (Quảng cáo)
Tọa độ giao điểm (-1 ; 3)
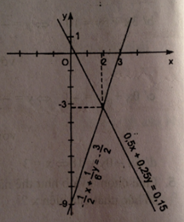
b) Vẽ đường thẳng 0,5x + 0,25y = 0,15 là đồ thị của hàm số
y = -2x + 0,6
Cho \(x = 0 \Rightarrow y = 0,6\) (0 ; 0,6)
Cho \(y = 0 \Rightarrow x = 0,3\) (0,3 ; 0)
Vẽ đường thẳng \( – {1 \over 2}x + {1 \over 6}y = – {3 \over 2}\) là đồ thị hàm số y = 3x – 9
Cho \(x = 0 \Rightarrow y = – 9\) (0 ; -9)
Cho \(y = 0 \Rightarrow x = 3\) (3 ; 0)
Hoành độ giao điểm của 2 đường thẳng:
\(\eqalign{
& – 2x + 0,6 = 3x – 9 \Leftrightarrow 5x = – 9,6 \cr
& \Leftrightarrow x = 1,92 \cr} \)
Advertisements (Quảng cáo)
Tung độ giao điểm: y = 3.1,92 – 9 = -3,24
Tọa độ giao điểm (1,92 ; -3,24)
c) Vẽ đường thẳng 4x + 5y = 20 là đồ thị hàm số y = -0,8 + 4
Cho \(x = 0 \Rightarrow y = 4\) (0 ; 4)
Cho \(y = 0 \Rightarrow x = 5\) (5 ; 0)
Vẽ đường thẳng 0,8x + y = 4 là đồ thị hàm số y = -0,84 + 4
Hai đường thẳng đó trùng nhau có vô số điểm chung
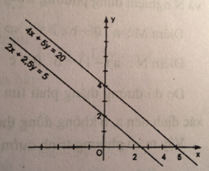
d) Vẽ đường thẳng 4x + 5y = 20 là đồ thị hàm số y = -0,8x + 4
Cho \(x = 0 \Rightarrow y = 4\) (0 ; 4)
Cho \(y = 0 \Rightarrow x = 5\) (5 ; 0)
Vẽ đường thẳng 2x + 2,5y = 5 là đồ thị hàm số y = -0,8x + 2
Cho \(x = 0 \Rightarrow y = 2\) (0 ; 2)
Cho \(y = 0 \Rightarrow x = 2,5\) (2,5 ; 0)
Hai đường thẳng có hệ số góc bằng nhau, tung độ gốc khác nhau, chúng song song không có tọa giao điểm.
Câu 7: Giải thích vì sao khi \(M\left( {{x_0};{y_0}} \right)\) là giao điểm của 2 đường thẳng ax + by = c và a’x + b’y = c’ thì \(\left( {{x_0};{y_0}} \right)\) là nghiệm chung của 2 phương trình ấy.
Điểm \(M\left( {{x_0};{y_0}} \right)\) là giao điểm của 2 đường thẳng ax + by = c và a’x + b’y = c’
Vì điểm M thuộc đường thẳng ax + by = c nên tọa độ của nó nghiệm đúng phương trình đường thẳng này, ta có: \(a{x_0} + b{y_0} = c\)
Vì M thuộc đường thẳng a’x + b’y = c’ nên tọa độ của nó nghiệm đúng phương trình đường thẳng này, ta có: \(a'{x_0} + b'{y_0} = c’\)
Vậy \(\left( {{x_0};{y_0}} \right)\) là nghiệm chung của 2 đường thắng ax + by = c và a’x + b’y = c’.

