Câu 1: Hãy tính x và y trong các hình sau
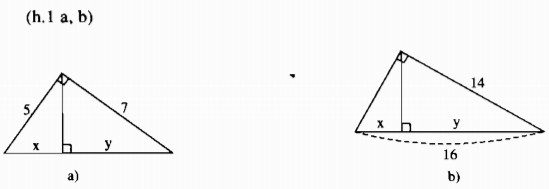

a) hình a
Theo định lý Pi-ta-go, ta có:
\(x + y = \sqrt {{5^2} + {7^2}} = \sqrt {74} \)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu của nó, ta có:
\({5^2} = x.(x + y) \Rightarrow x = {{{5^2}} \over {x + y}} = {{25} \over {\sqrt {74} }}\)
Thay \(x = {{25} \over {\sqrt {74} }}\) vào \(x + y = \sqrt {74} \), ta có:
\({{25} \over {\sqrt {74} }} + y = \sqrt {74} \Rightarrow y = \sqrt {74} – {{25} \over {\sqrt {74} }} = {{74 – 25} \over {\sqrt {74} }} = {{49} \over {\sqrt {74} }}\)
b. Hình b
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\({14^2} = y.16 \Rightarrow y = {{{{14}^2}} \over {16}} = {{196} \over {16}} = 12,25\)
\(x + y = 16 \Rightarrow x = 16 – y = 16 – 12,25 = 3,75\)
Câu 2: Hãy tính x và y trong các hình sau


a) Hình a
Advertisements (Quảng cáo)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\({x^2} = 2.(2 + 6) = 2.8 = 16 \Rightarrow x = 4\)
\({y^2} = 6.(2 + 6) = 6.8 = 48 \Rightarrow y = \sqrt {48} = 4\sqrt 3 \)
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu hai cạnh góc vuông, ta có:
\({x^2} = 2.8 = 16 \Rightarrow x = 4\)
Câu 3: Hãy tính x và y trong các hình sau
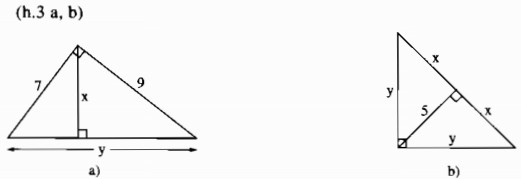

a) Hình a
Theo định lý Pi-ta-go, ta có:
Advertisements (Quảng cáo)
\({y^2} = {7^2} + {9^2} \Rightarrow y = \sqrt {{7^2} + {9^2}} = \sqrt {130} \)
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
\(x.y = 7.9 \Rightarrow x = {{7.9} \over y} = {{63} \over {\sqrt {130} }}\)
b) Hình b
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\({5^2} = x.x = {x^2} \Rightarrow x = 5\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\({y^2} = x.(x + x) = 5.(5 + 5) = 50 \Rightarrow y = \sqrt {50} = 5\sqrt 2 \)
Câu 4: Hãy tính x và y trong các hình sau
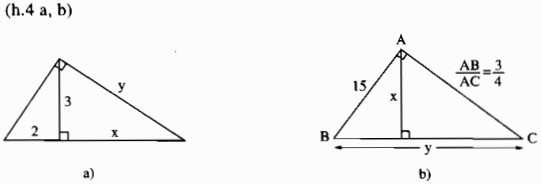

a) Hình a
Theo hệ thức liên hệ giữa đường cao và hình chiếu, ta có:
\({3^2} = 2.x \Rightarrow x = {{{3^2}} \over 2} = {9 \over 2} = 4,5\)
Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu, ta có:
\(\eqalign{
& {y^2} = x.(x + 2) = 4,5.(4,5 + 2) = 29,25 \cr
& \Rightarrow y = \sqrt {29,25} \cr} \)
b) Hình b
Ta có:
\(\eqalign{
& {{AB} \over {AC}} = {3 \over 4} \Rightarrow {{AB} \over 3} = {{AC} \over 4} \cr
& \Rightarrow AC = 4.{{AB} \over 3} = 4.{{15} \over 3} = 4.5 = 20 \cr} \)
Theo định lý Pi-ta-go, ta có:
\({y^2} = B{C^2} = A{B^2} + A{C^2} = {15^2} + {20^2} = 625\)
Suy ra:
\(y = \sqrt {625} = 25\)
Theo hệ thức liên hệ giữa đường cao và cạnh trong tam giác vuông, ta có:
\(\eqalign{
& x.y = 15.20 \cr
& \Rightarrow x = {{15.20} \over y} = {{15.20} \over {25}} = 12 \cr} \)

